题目内容
9.观察下列关于自然数的等式:①32-4×12=5;②52-4×22=9;②72-4×32=13.
请你猜想第n个等式为(用含n的式子表示)(2n+1)2-4n2=4n+1.
分析 由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.
解答 解:(1)32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
所以第n个等式为:(2n+1)2-4n2=4n+1,
故答案为:(2n+1)2-4n2=4n+1.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
4.若方程组$\left\{\begin{array}{l}{9x+4y=1}\\{x+6y=-11}\end{array}\right.$的解x,y满足2x-ky=10,则k的值是( )
| A. | -4 | B. | 6 | C. | 4 | D. | -6 |
1.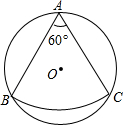 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{3}}{6}$m | B. | $\frac{\sqrt{3}}{12}$m | C. | $\frac{\sqrt{3}}{2}$m | D. | 1m |

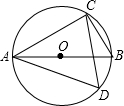 如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.
如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.