题目内容
13.已知二次函数y=a(x-h)2+k的图象的顶点坐标为(-1,2),且与y=-$\frac{1}{2}$x2的图象的开口方向、形状均相同.(1)求这个函数的表达式;
(2)分析所求函数的图象能否由抛物线y=-$\frac{1}{2}$x2平移得到?若能,说出你的平移方法;
(3)另有一点A(m,-m2),请你分析点A是否在这个函数的图象上,为什么?
分析 (1)根据已知即可求出h、k、a的值,即可求出答案;
(2)根据解析式和平移规律得出即可;
(3)把A的坐标代入解析式,看看两边是否相等即可.
解答 解:(1)∵二次函数y=a(x-h)2+k的图象的顶点坐标为(-1,2),且与y=-$\frac{1}{2}$x2的图象的开口方向、形状均相同,
∴h=-1,k=2,a=-$\frac{1}{2}$,
∴这个函数的表达式是y=-$\frac{1}{2}$(x+1)2+2;
(2)所求函数的图象能由抛物线y=-$\frac{1}{2}$x2平移得到,平移方法是把函数y=-$\frac{1}{2}$x2的图象向左平移1个长度单位,再向上平移2个长度单位即可得出函数y=-$\frac{1}{2}$(x+1)2+2的图象;
(3)A不在这个函数的图象上
理由是:把A(m,-m2)代入y=-$\frac{1}{2}$(x+1)2+2得:左边=-m2,右边=-$\frac{1}{2}$(m+1)2+2=-$\frac{1}{2}$m2-m-$\frac{1}{2}$+2=-$\frac{1}{2}$m2-m+$\frac{3}{2}$,
左边≠右边,
所以A不在这个函数的图象上.
点评 本题考查了求二次函数的图象,平移的性质,二次函数图象上点的坐标特征的应用,能综合运用知识点进行计算是解此题的关键,注意:左加右减,上加下减.

练习册系列答案
相关题目
4.若方程组$\left\{\begin{array}{l}{9x+4y=1}\\{x+6y=-11}\end{array}\right.$的解x,y满足2x-ky=10,则k的值是( )
| A. | -4 | B. | 6 | C. | 4 | D. | -6 |
1.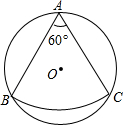 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{3}}{6}$m | B. | $\frac{\sqrt{3}}{12}$m | C. | $\frac{\sqrt{3}}{2}$m | D. | 1m |
7.下列式子中,是不等式的有( )
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
①2x=7;②3x+4y;③-3<2;④2a-3≥0;⑤x>1;⑥a-b>1.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 1个 |
 如图所示,⊙O中AB和AC的中点分别为点E和点F,直线EF交AC于点P,交AB于点Q,那么△APQ是什么三角形?并证明你的结论.
如图所示,⊙O中AB和AC的中点分别为点E和点F,直线EF交AC于点P,交AB于点Q,那么△APQ是什么三角形?并证明你的结论.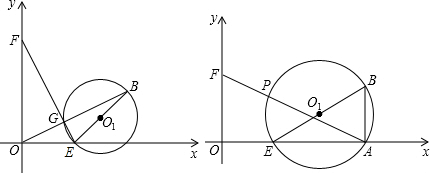
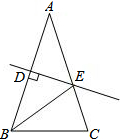 如图,等腰三角形ABC的周长为23,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为14.
如图,等腰三角形ABC的周长为23,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为14. 如图所示,△ABC≌△DEF.若∠B=26°,∠F=74°,则∠1=26°,∠2=74°,∠A=80°,∠D=80°.
如图所示,△ABC≌△DEF.若∠B=26°,∠F=74°,则∠1=26°,∠2=74°,∠A=80°,∠D=80°.