题目内容
14. 如图,四边形ABCD是平行四边形,连接对角线AC,E、F是对角线AC上两点,满足AE=CF,求证:四边形DEBF是平行四边形.
如图,四边形ABCD是平行四边形,连接对角线AC,E、F是对角线AC上两点,满足AE=CF,求证:四边形DEBF是平行四边形.
分析 首先连接BD,交AC于点O,由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OA=OC,OB=OD,又由AE=CF,可得OE=OF,然后根据对角线互相相平分的四边形是平行四边形.
解答 证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.

练习册系列答案
相关题目
1.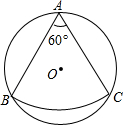 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
 如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )
如图,从一块半径是1m的圆形铁皮(⊙O)上剪出一个圆心角为60°的扇形(点A,B,C在⊙O上),将剪下的扇形围成一个圆锥,则这个圆锥的底面圆的半径是( )| A. | $\frac{\sqrt{3}}{6}$m | B. | $\frac{\sqrt{3}}{12}$m | C. | $\frac{\sqrt{3}}{2}$m | D. | 1m |
19.下列计算正确的是( )
| A. | (a5)2=a7 | B. | a5•a2=a10 | C. | (a3)2=a6 | D. | a2+a2=a4 |
4.下列调查方式,合适的是( )
| A. | 要了解一批灯泡的使用寿命,选择全面调查 | |
| B. | 要了解某市初中生的“体重指数”,选择全面调查 | |
| C. | 要了解湖南卫视“我是歌手”的收视率,选择抽样调查 | |
| D. | 要了解某班20名学生的视力状况,选择抽样调查 |
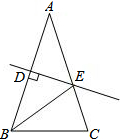 如图,等腰三角形ABC的周长为23,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为14.
如图,等腰三角形ABC的周长为23,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为14. 如图所示,△ABC≌△DEF.若∠B=26°,∠F=74°,则∠1=26°,∠2=74°,∠A=80°,∠D=80°.
如图所示,△ABC≌△DEF.若∠B=26°,∠F=74°,则∠1=26°,∠2=74°,∠A=80°,∠D=80°.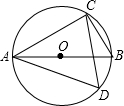 如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.
如图,已知AB为⊙O的直径,∠CAB=30°,则∠ADC=60度.