题目内容
10.已知5a2-4a-3=0,3b2+4b-5=0,且ab≠1,则2a+$\frac{2}{b}+\frac{a}{b}$的值为1.分析 先把方程3b2+4b-5=0的两边都除以b2得到5•($\frac{1}{b}$)2-4•$\frac{1}{b}$-3=0,加上5a2-4a-3=0,于是可把a和$\frac{1}{b}$看作方程5x2-4x-3=0的两实数解,然后根据根与系数的关系求解.
解答 解:∵3b2+4b-5=0,
∴5•($\frac{1}{b}$)2-4•$\frac{1}{b}$-3=0,
∵5a2-4a-3=0,
∴a和$\frac{1}{b}$可看作方程5x2-4x-3=0的两实数解,
∴a•$\frac{1}{b}$=-$\frac{3}{5}$,a+$\frac{1}{b}$=$\frac{4}{5}$,
即$\frac{a}{b}$=-$\frac{3}{5}$,
∴2a+$\frac{2}{b}+\frac{a}{b}$=2(a+$\frac{1}{b}$)+$\frac{a}{b}$=2×$\frac{4}{5}$-$\frac{3}{5}$=1,
故答案为1.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
5.若|a|=2,b的相反数是最大的负整数,c是绝对值最小的数,则-a+b-c的值为( )
| A. | 0 | B. | 3或-1 | C. | 2 | D. | -1 |
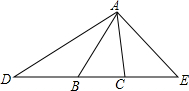 如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形.
如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形. 如图,已知在△ABC中,DE∥BA,DF∥CA,求证:$\frac{CM}{DM}=\frac{CD}{BD}$.
如图,已知在△ABC中,DE∥BA,DF∥CA,求证:$\frac{CM}{DM}=\frac{CD}{BD}$.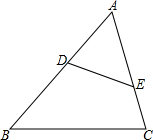 已知:如图,在△ABC中,点D、E分别在AB、AC上,且∠AED=∠B.
已知:如图,在△ABC中,点D、E分别在AB、AC上,且∠AED=∠B.