题目内容
20．在-$\sqrt{3}$，-2，0，1这四个数中，最小的数是（ ）| A． | -$\sqrt{3}$ | B． | -2 | C． | 0 | D． | 1 |
分析 根据实数的大小比较法则比较即可．
解答 解：在-$\sqrt{3}$，-2，0，1这四个数中，最小的数是-2，
故选B．
点评 本题考查了实数的大小比较法则，能熟记法则的内容是解此题的关键．
练习册系列答案
口算能手系列答案
相关题目
11．
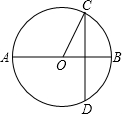如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）
如图，AB是⊙O的直径，弦CD⊥AB，∠OCD=30°，CD=2$\sqrt{3}$，则扇形BOC的面积为（ ）| A． | $\frac{2π}{3}$ | B． | $\frac{π}{3}$ | C． | π | D． | 2π |
15．
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）
如图，在平面直角坐标系中，Rt△ABO中，∠ABO=90°，OB边在x轴上，将△ABO绕点B顺时针旋转60°得到△CBD．若点A的坐标为（-2，2$\sqrt{3}$），则点C的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，$\sqrt{3}$） | C． | （1，2） | D． | （2，1） |
5．
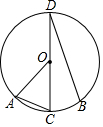如图，CD是圆O的直径，AC，BD是弦，C是弧AB的中点，且∠BDC=25°，则∠AOC的度数是（ ）
如图，CD是圆O的直径，AC，BD是弦，C是弧AB的中点，且∠BDC=25°，则∠AOC的度数是（ ）| A． | 25° | B． | 45° | C． | 50° | D． | 60° |
12．从-2，-1，-$\frac{1}{2}$，1，2这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组$\left\{\begin{array}{l}{2x+7≥9}\\{x-a＜0}\end{array}\right.$无解，且使分式方程$\frac{a}{2x-3}$+$\frac{a-2}{2x-3}$=-1的解为正分数，那么这五个数中所有满足条件的a的值之和是（ ）
| A． | -3 | B． | -$\frac{5}{2}$ | C． | -2 | D． | -$\frac{7}{2}$ |
9．下列说法中正确的有（ ）
①过一点有且只有一条直线与已知直线垂直；
②如果两个角相等，那么这两个角是对顶角；
③如果两条直线被第三条直线所截，那么内错角相等；
④联结直线外一点与直线上各点的所有线段，垂线段最短；
⑤邻补角的平分线互相垂直．
①过一点有且只有一条直线与已知直线垂直；
②如果两个角相等，那么这两个角是对顶角；
③如果两条直线被第三条直线所截，那么内错角相等；
④联结直线外一点与直线上各点的所有线段，垂线段最短；
⑤邻补角的平分线互相垂直．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
10．若一元二次方程x2+2x+m=0没有实数根，则m的取值范围是（ ）
| A． | m≥1 | B． | m≤1 | C． | m＞1 | D． | m＜1 |