题目内容
5.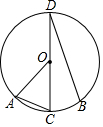 如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )
如图,CD是圆O的直径,AC,BD是弦,C是弧AB的中点,且∠BDC=25°,则∠AOC的度数是( )| A. | 25° | B. | 45° | C. | 50° | D. | 60° |
分析 根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半可得∠AOC=2∠CDB,进而可得答案.
解答 解:∵C是弧AB的中点,
∴$\widehat{AC}$=$\widehat{BC}$,
∴∠AOC=2∠CDB,
∵∠BDC=25°,
∴∠AOC=50°,
故选:C.
点评 此题主要考查了圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{24}÷\sqrt{3}=4$ | D. | $\sqrt{(-3)^{2}}=-3$ |
16.我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.下面四边形是等对角线四边形的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 梯形 |
20.在-$\sqrt{3}$,-2,0,1这四个数中,最小的数是( )
| A. | -$\sqrt{3}$ | B. | -2 | C. | 0 | D. | 1 |
10.在Rt△ABC中,∠C=90°,a=3,c=5,则sinA的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
17. 如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
 如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )
如图,在△ABC中,AB=AC,D为BC边上一点,且AD=AE,则∠BAD与∠EDC的关系为( )| A. | ∠BAD=∠EDC | B. | ∠BAD=2∠EDC | C. | ∠BAD+∠EDC=45° | D. | ∠BAD+∠EDC=60° |
15.2016年2月初,合肥市教育考试院召开新闻发布会,公布了合肥市市区参加2016年中考的学生约为27600人,与去年相比增加300多人,用科学记数法表示“27600”正确的( )
| A. | 2.76×103 | B. | 2.76×104 | C. | 2.76×105 | D. | 0.276×105 |
 如图,求证:∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.
如图,求证:∠A+∠B+∠C+∠D+∠E+∠F+∠G=180°.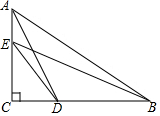 如图,在△ABC中,∠C=90°,点D,E分别在边BC,AC上,若DE=$\sqrt{5}$,AB=5,求AD2+BE2的值.
如图,在△ABC中,∠C=90°,点D,E分别在边BC,AC上,若DE=$\sqrt{5}$,AB=5,求AD2+BE2的值.