题目内容
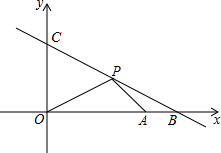 在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.
在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.(1)分别求出B、C的坐标;
(2)求S关于x的函数解析式,并写出x的取值范围;
(3)若在坐标系中有一点Q(a,2),且△QAC的面积与△OBC的面积相等,求a的值.
考点:一次函数综合题
专题:
分析:(1)令y=0,则x=4,令x=0,则y=4,即可求得B、C的坐标;
(2)根据三角形的面积公式和P的坐标即可表示出关于x的函数解析式;
(3)△QAC的面积等于三角形CQG与四边形OBQG的面积的和减去三角形OAC的面积,根据△QAC的面积与△OBC的面积相等,即可得出关于a的一元一次方程,解方程即可求得.
(2)根据三角形的面积公式和P的坐标即可表示出关于x的函数解析式;
(3)△QAC的面积等于三角形CQG与四边形OBQG的面积的和减去三角形OAC的面积,根据△QAC的面积与△OBC的面积相等,即可得出关于a的一元一次方程,解方程即可求得.
解答:解:(1)令y=0,则0=-x+4,得:x=4,
∴B(4,0),
令x=0,则y=4,
∴C(0,4),
(2)∵S=
OA•y,
∴S=
×3y,
∵点P(x,y)在直线l上,
∴S=
(-x+4)=-
x+6,
即S=-
x+6,(0<x<4);
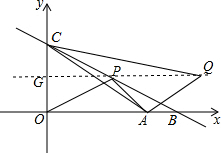
(3)如图,∵Q(a,2),
∴过Q点作x轴的平行线交y轴的交点G(0,2),
∵S△OBC=
OB•OC=
×4×4=8,S△CQG=
GQ•GC=
a×2=a,S四边形OAQG=
(OA+GQ)•OG=
(a+3)×2=a+3,S△OAC=
OA•OC=
×3×4=6,
又∵△QAC的面积与△OBC的面积相等,
∴S△CQG+S四边形OAQG-S△OAC=8,
即a+a+3-6=8,解得:a=
.
∴B(4,0),
令x=0,则y=4,
∴C(0,4),
(2)∵S=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
∵点P(x,y)在直线l上,
∴S=
| 3 |
| 2 |
| 3 |
| 2 |
即S=-
| 3 |
| 2 |

(3)如图,∵Q(a,2),
∴过Q点作x轴的平行线交y轴的交点G(0,2),
∵S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵△QAC的面积与△OBC的面积相等,
∴S△CQG+S四边形OAQG-S△OAC=8,
即a+a+3-6=8,解得:a=
| 11 |
| 2 |
点评:本题考查了一次函数与坐标轴的交点坐标,直线上的点的特点,三角形的面积,以及分割法求三角形的面积的方法等,(3))△QAC的面积等于三角形CQG与四边形OBQG的面积的和减去三角形OAC的面积是本题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
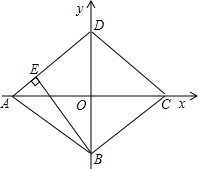 已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.
已知直角坐标系中菱形ABCD的位置如图,且C(4,0)、D(0,3).现有两动点P、Q分别从A、C同时出发,点P沿线段AD向终点D运动,点Q沿折线CBA向终点A运动,设运动时间为t秒.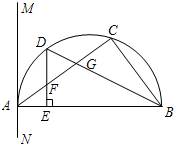 如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
如图,△ABC内接于半圆,AB是直径,过点A作直线MN,使∠MAC=∠ABC,D是
 如图,AD∥BC,∠A=90°,点E是AB上的一点,∠1=∠2,AE=BC,请你说明∠DEC=90°的理由.
如图,AD∥BC,∠A=90°,点E是AB上的一点,∠1=∠2,AE=BC,请你说明∠DEC=90°的理由. 如图,在△ABC中,∠B=64°,∠BAC=72°,D为BC上一点,DE交AC于点F,且AB=AD=DE,连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
如图,在△ABC中,∠B=64°,∠BAC=72°,D为BC上一点,DE交AC于点F,且AB=AD=DE,连接AE,∠E=55°,请判断△AFD的形状,并说明理由. Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=
Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=