题目内容
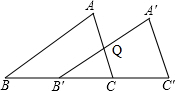 Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=
Rt△A′B′C′是Rt△ABC沿BC方向平移得到的,若BC=6cm,B′Q=| 1 |
| 2 |
| 1 |
| 4 |
考点:平移的性质
专题:
分析:设AC与A′B′相交于点D,根据平移的性质判定△ABC与△B′CD相似,然后根据相似三角形面积的比等于相似比的平方求出B′C的长度,再根据BB′=BC-B′C,计算即可得解.
解答:解:根据平移的性质,AB∥A′B′,
∴△QB′C∽△ABC,
∵S△QB′C=
S△ABC,
∴(
)2=
,
∵BC=6cm,
∴B′C=,
∴BB′=BC-B′C=6-3=3cm.
故答案为:3cm.
∴△QB′C∽△ABC,
∵S△QB′C=
| 1 |
| 4 |
∴(
| B′C |
| BC |
| 1 |
| 4 |
∵BC=6cm,
∴B′C=,
∴BB′=BC-B′C=6-3=3cm.
故答案为:3cm.
点评:本题考查了平移的性质,相似三角形的判定与性质,判定出两三角形相似,利用相似三角形面积的比等于相似比的平方求出B′C的长度是解题的关键.

练习册系列答案
相关题目
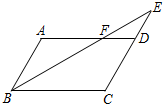 如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )
如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,若CD=2DE,则AF:FD的值为( )| A、3:2 | B、2:3 |
| C、2:1 | D、3:1 |
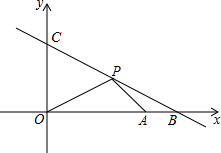 在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.
在直角坐标系xOy中,已知点A(3,0),直线l:y=-x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设△OPA的面积为S.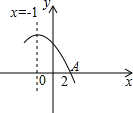 已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是
已知二次函数y=ax2+bx+c的部分图象如图,其对称轴为直线x=-1.若其与x轴的一个交点为A(2,0),则由图象可知,当自变量x的取值范围是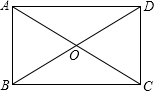 如图,矩形ABCD的两条对角线相交于点O,AB=2
如图,矩形ABCD的两条对角线相交于点O,AB=2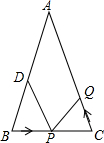 如图,在△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为
如图,在△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点,如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,当点Q的运动速度为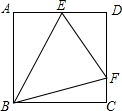 如图,在正方形ABCD中,点E是AD边的中点,F是CD边上一点,且∠EBF=45°,则tan∠EFB的值为
如图,在正方形ABCD中,点E是AD边的中点,F是CD边上一点,且∠EBF=45°,则tan∠EFB的值为