题目内容
18.对于抛物线y=$\frac{1}{2}$(x+2)2+1的下列描述中,错误是( )| A. | 对称轴为x=-2,顶点坐标为(-2,1) | |
| B. | 当x<-2时,函数值y随x值的增大而减小 | |
| C. | 当x=2时,有最大值为1 | |
| D. | 当x>-2时,函数值y随x值的增大而增大 |
分析 由解析式可求得其开口方向、对称轴及顶点坐标,可知其有最小值,再结合二次函数的增减性可求得答案.
解答 解:
∵y=$\frac{1}{2}$(x+2)2+1,
∴抛物线对称轴为x=-2,顶点坐标为(-2,1),故A正确;
∵a=$\frac{1}{2}$>0,
∴抛物线开口向上,
∴当x=-2时,函数有最小值,故C不正确;
∴当x<-2时,函数y随x的增大而减小,当x>-2时,函数y随x的增大而增大,
故B、D正确;
故选C.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
相关题目
9.已知点A(-1-$\sqrt{2}$,y1)、B(-1,y2)、C(2,y3)在抛物线y=(x-1)2+c上,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y3>y1 |
 如图是一个三角形点阵图,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点,容易看出,10是三角点阵中前4行的点数和,则300个点是前24行的点数和.
如图是一个三角形点阵图,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点,容易看出,10是三角点阵中前4行的点数和,则300个点是前24行的点数和.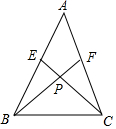 如图,AB=AC,AE=AF.
如图,AB=AC,AE=AF.