题目内容
15.2016年9月28第七届安徽省花博会在阜阳开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的柳编工艺品投放市场进行试销.阜阳市物价部门规定该工艺品销售单价不得低于成本价,最高不能超过38元/件,经过调查,得到如表数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,该厂试销该工艺品每天所获利润最大?最大利润是多少?
(3)若该工艺厂要获得的利润不低于8000元,试确定销售单价x的取值范围.
分析 (1)根据表格中的数据可以求得一次函数中k、b的值,从而可以求出一次函数的解析式;
(2)根据题意可以写出利润w与x的函数关系式,从而可以求得最大利润,注意x的取值范围;
(3)根据题意可以得到关于x的不等式,从而可以求得x的取值范围,注意题目中对x的限制.
解答 解:(1)∵y与x是一次函数关系y=kx+b,
∴$\left\{\begin{array}{l}{20k+b=500}\\{30k+b=400}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-10}\\{b=700}\end{array}\right.$,
即这个一次函数的关系式为:y=-10x+700;
(2)设利润为w,
w=(x-10)(-10x+700)=-10(x-40)2+9000,
∵10≤x≤38,
∴当x=38时,w取得最大值,此时w=-10(38-40)2+9000=8960,
即当销售单价定为38元时,该厂试销该工艺品每天所获利润最大,最大利润是8960元;
(3)由题意可得,
-10(x-40)2+9000≥8000,
解得,30≤x≤50,
又∵10≤x≤38,
∴30x≤38,
即若该工艺厂要获得的利润不低于8000元,则销售单价x的取值范围是30x≤38.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
5.反比例函数y=$\frac{2-3k}{x}$的图象经过点(-2,5),则k的值为( )
| A. | 10 | B. | -10 | C. | 4 | D. | -4 |
 如图是一个三角形点阵图,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点,容易看出,10是三角点阵中前4行的点数和,则300个点是前24行的点数和.
如图是一个三角形点阵图,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点,容易看出,10是三角点阵中前4行的点数和,则300个点是前24行的点数和.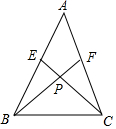 如图,AB=AC,AE=AF.
如图,AB=AC,AE=AF.