题目内容
 画图题:
画图题:直线AB,CD相交于点O,∠BOC=60°,点P在直线CD上,
(1)利用学习用具过点P画PE∥AB,并说明理由.
(2)过点P画AB的垂线段PE,垂足为E.
(3)过点P画CD的垂线,与AB相交于F点.
(4)说明线段PE、PO、FO三者的大小关系,其依据是什么?
考点:作图—基本作图
专题:
分析:(1)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和已知点重合,过已知点沿三角板的直角边画直线即可;
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可;
(3)把三角板的一条直角边与已知直线CD重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可;
(4)利用直角三角形斜边长大于直角边长得出即可.
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可;
(3)把三角板的一条直角边与已知直线CD重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和P点重合,过P点沿三角板的直角边画直线即可;
(4)利用直角三角形斜边长大于直角边长得出即可.
解答: 解:(1)如图所示:PR即为所求;
解:(1)如图所示:PR即为所求;
(2)如图所示:PE即为所求;
(3)如图所示:PF即为所求;
(4)∵∠PEO=90°,
∴PO>PE,
∵∠POF=60°,∠OPF=90°,
∴∠PFO=30°,
∴PF>PO,
∴PF>PO>PE.
 解:(1)如图所示:PR即为所求;
解:(1)如图所示:PR即为所求;(2)如图所示:PE即为所求;
(3)如图所示:PF即为所求;
(4)∵∠PEO=90°,
∴PO>PE,
∵∠POF=60°,∠OPF=90°,
∴∠PFO=30°,
∴PF>PO,
∴PF>PO>PE.
点评:本题考查了基本作图以及直角三角形的性质等知识,培养了学生过直线外一点作已知直线的平行线和垂线的画图能力.

练习册系列答案
相关题目
若三角形两条边的长分别为1、5,则第三条边的长可以是( )
| A、1 | B、3 | C、5 | D、7 |
下列计算正确的是( )
| A、2x+3y=5xy |
| B、x4•x4=x16 |
| C、(4x8)÷(2x2)=2x6 |
| D、(a3)2•a4=a9 |
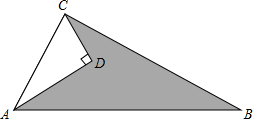 如图的一块地(图中阴影部分),∠ADC=90°,AD=12,CD=9,AB=25,BC=20.
如图的一块地(图中阴影部分),∠ADC=90°,AD=12,CD=9,AB=25,BC=20.
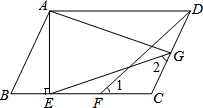 已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.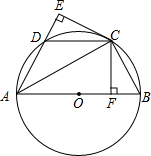 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.