题目内容
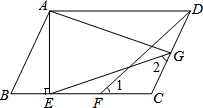 已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.(1)求证:G为CD的中点.
(2)若CF=2,AE=3,求BE的长.
考点:平行四边形的性质
专题:
分析:(1)通过证△ECG≌△DCF得到CG=CF,结合已知条件知CG=
CD,即G为CD的中点.
(2)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可.
| 1 |
| 2 |
(2)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可.
解答:(1)证明:如图,∵点F为CE的中点,
∴CF=
CE
在△ECG与△DCF中,
,
∴△ECG≌△DCF(AAS),
∴CG=CF=
CE.
又CE=CD,
∴CG=
CD,即G为CD的中点;
(2)解:∵CE=CD,点F为CE的中点,CF=2,
∴DC=CE=2CF=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=
=
.
∴CF=
| 1 |
| 2 |
在△ECG与△DCF中,
|
∴△ECG≌△DCF(AAS),
∴CG=CF=
| 1 |
| 2 |
又CE=CD,
∴CG=
| 1 |
| 2 |
(2)解:∵CE=CD,点F为CE的中点,CF=2,
∴DC=CE=2CF=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=
| 42-32 |
| 7 |
点评:本题考查了平行四边形性质,全等三角形的性质和判定等知识点的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
下列运算,正确的是( )
| A、a+a=a2 |
| B、a•a=2a |
| C、3a3-2a2=a |
| D、2a•3a2=6a3 |
下列图象中,表示直线y=x+1的是( )
A、 |
B、 |
C、 |
D、 |
 画图题:
画图题: △ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度. 如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动(点E不与B、C重合),连结AE、DE,以AE为边作矩形AG,使边FG过点D.
如图,已知矩形ABCD,动点E从点B沿线段BC向点C运动(点E不与B、C重合),连结AE、DE,以AE为边作矩形AG,使边FG过点D.