题目内容
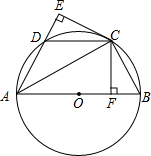 已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且CB=CD,CF⊥AB于点F,CE⊥AD的延长线于点E.(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求CF的长.
考点:全等三角形的判定与性质,角平分线的性质,圆心角、弧、弦的关系,圆周角定理
专题:
分析:(1)由CB=CD,根据等弦对的圆周角相等,得到一对角相等,继而得到AC为角平分线,利用角平分线定理得到CE=CF,利用HL得到三角形CDE与三角形CBF全等,利用全等三角形对应边相等即可得证;
(2)根据AC为角平分线,且∠DAB=60°,得到∠BAC=30°,在直角三角形ABC中,利用30度所对的直角边等于斜边的一半求出BC的长,利用勾股定理求出AC的长,在直角三角形ACF中,利用30度所对的直角边等于斜边的一半即可求出CF的长.
(2)根据AC为角平分线,且∠DAB=60°,得到∠BAC=30°,在直角三角形ABC中,利用30度所对的直角边等于斜边的一半求出BC的长,利用勾股定理求出AC的长,在直角三角形ACF中,利用30度所对的直角边等于斜边的一半即可求出CF的长.
解答:(1)证明:∵CB=CD,
∴∠BAC=∠EAC,
∵CE⊥AE,CF⊥AF,
∴CE=CF,
在Rt△CED和Rt△CFB中,
,
∴Rt△CED≌Rt△CFB(HL),
则DE=BF;
(2)∵∠BAC=∠EAC,且∠DAB=60°,
∴∠BAC=∠EAC=30°,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,AB=6,
∴BC=
AB=3,
根据勾股定理得:AC=
=3
,
在Rt△ACF中,CF=
AC=
.
∴∠BAC=∠EAC,
∵CE⊥AE,CF⊥AF,
∴CE=CF,
在Rt△CED和Rt△CFB中,
|
∴Rt△CED≌Rt△CFB(HL),
则DE=BF;
(2)∵∠BAC=∠EAC,且∠DAB=60°,
∴∠BAC=∠EAC=30°,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,AB=6,
∴BC=
| 1 |
| 2 |
根据勾股定理得:AC=
| 62-32 |
| 3 |
在Rt△ACF中,CF=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题考查了全等三角形的判定与性质,圆周角定理,圆心角、弦及弧之间的关系,以及角平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对60个数据进行处理时,适当分组,各组数据个数之和与百分率之和分别等于( )
| A、60,1 | B、60,60 |
| C、1,60 | D、1,1 |
 画图题:
画图题: 如图,已知在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=78°,求∠DAC的度数.
如图,已知在△ABC中,D是BC边上一点,∠1=∠B,∠2=∠C,∠BAC=78°,求∠DAC的度数. △ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.
△ABC在平面直角坐标系中的位置如图,其中每个小正方形的边长为1个单位长度.