题目内容
若三角形两条边的长分别为1、5，则第三条边的长可以是（ ）
| A、1 | B、3 | C、5 | D、7 |
考点：三角形三边关系
专题：
分析：首先根据三角形的三边关系定理可得5-1＜x＜5+1，解出不等式的解集，再选取符合条件的数即可．
解答：解：设第三边长为x，根据三角形的三边关系可得：
5-1＜x＜5+1，
即4＜x＜6，
故选：C．
5-1＜x＜5+1，
即4＜x＜6，
故选：C．
点评：此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
练习册系列答案
53随堂测系列答案
相关题目
已知锐角A满足关系式：（2sinA+1）（3sinA-1）=0，则sinA=（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、30° |
若直角三角形的两直角边长分别为5cm，12cm，则这个直角三角形的斜边长是（ ）
| A、13cm | ||
B、
| ||
| C、169cm | ||
| D、12cm |
把不等式组
的解在数轴上表示出来，正确的是（ ）
|
A、 |
B、 |
C、 |
D、 |
下列运算，正确的是（ ）
| A、a+a=a2 |
| B、a•a=2a |
| C、3a3-2a2=a |
| D、2a•3a2=6a3 |
对60个数据进行处理时，适当分组，各组数据个数之和与百分率之和分别等于（ ）
| A、60，1 | B、60，60 |
| C、1，60 | D、1，1 |
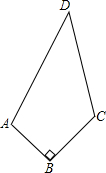如图，四边形ABCD中，AB=6cm，BC=8cm，CD=24cm，DA=26cm，且∠ABC=90°，则四边形ABCD的面积是（ ）cm2．| A、336 | B、144 |
| C、102 | D、无法确定 |
画图题：