题目内容
9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
分析 利用图象判定①;利用抛物线和直线都经过顶点A可判定②;利用顶点坐标判定③;利用待定系数法求得直线解析式,进而求得B的坐标,宽判定④.
解答 解:∵由图象可知,当x<1时,有y1<y2,故①正确;
∵抛物线的顶点坐标A(1,3),直线y2=mx+n(m≠0)经过A点,
∴当x=1时,y1=y2,
∴a+b+c=m+n,故②正确;
∵抛物线的最大值为$\frac{4ac-{b}^{2}}{4a}$=3,
∴4ac-b2=12a,
∴b2-4ac=-12a,故③正确;
∵抛物线经过A(1,3),
∴代入y2=mx+n得,m+n=3,
解$\left\{\begin{array}{l}{m+n=3}\\{m-n=-5}\end{array}\right.$得$\left\{\begin{array}{l}{m=-1}\\{n=4}\end{array}\right.$,
∴y2=-x+4,
令y=0,则x=4,
∴B(4,0),故④正确;
故选D.
点评 本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点,抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.
如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠ADE的度数为60°.
 BA与⊙O相切,切点为A,连接OB交⊙O于点C.
BA与⊙O相切,切点为A,连接OB交⊙O于点C.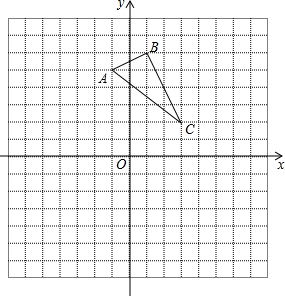 已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.
已知如图,在平面直角坐标系xOy中,A(-1,5),B(1,6),C(3,2),请在图中作出△ABC关于x轴的轴对称图形△A1B1C1.