题目内容
18.计算:(1)($\sqrt{24}+\sqrt{0.5}$)-($\sqrt{\frac{1}{8}}-\sqrt{6}$);
(2)(3$\sqrt{12}-2\sqrt{\frac{1}{3}}+\sqrt{48}$)$÷2\sqrt{3}$.
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(2)先把括号内各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算.
解答 解:(1)原式=2$\sqrt{6}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$+$\sqrt{6}$
=3$\sqrt{6}$+$\frac{\sqrt{2}}{4}$;
(2)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)÷2$\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$÷2$\sqrt{3}$
=$\frac{14}{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
9. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点为B,直线y2=mx+n(m≠0)经过A、B两点,下列结论:①当x<1时,有y1<y2;
②a+b+c=m+n;
③b2-4ac=-12a;
④若m-n=-5,则B点坐标为(4,0)
其中正确的是( )
| A. | ① | B. | ①② | C. | ①②③ | D. | ①②③④ |
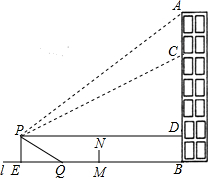 如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.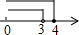

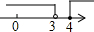
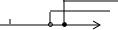
 解是__________.
解是__________.