如图所示.在Rt△ABC中.已知∠A=90°.AB=6.BC=8cm.DE垂直平分BC.则BE的长是( )A．3cmB．4cmC．5cmD．以上答案都不对题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图所示，在Rt△ABC中，已知∠A=90°，AB=6，BC=8cm，DE垂直平分BC，则BE的长是（　　）

A．

3cm

B．

4cm

C．

5cm

D．

以上答案都不对

分析连接CE，根据勾股定理求出AC的长，根据线段的垂直平分线的性质得到BE=CE，根据勾股定理列出方程，解方程即可．

解答解：连接CE，
∵AB=6cm，BC=8cm，
∴AC²=BC²-AB²=28，
∵DE垂直平分BC，
∴BE=CE，
设BE=xcm，则CE=xcm，AE=AB-BE=6-x（cm），
∵AE²+AC²=CE²，
∴（6-x）²+28=x²，
解得：x=$\frac{16}{3}$，
故选：D．

点评本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．

练习册系列答案

9．已知a+b=-4，2ab=3，则$\sqrt{\frac{b}{2a}}$+$\sqrt{\frac{2a}{b}}$=2$\sqrt{3}$-$\frac{\sqrt{30}}{6}$或2$\sqrt{3}$+$\frac{\sqrt{30}}{6}$．．

13．

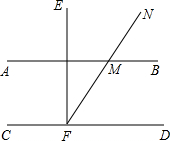如图，AB∥CD，EF⊥CD于点F，射线FN交AB于点M，∠NMB=57°，则∠EFN=33°．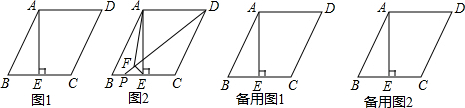

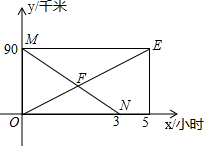20．如图1，在?ABCD中，AE⊥BC于E，E恰为BC的中点，AE=2BE
（1）求证：AD=AE；
（2）如图2，点P在BE上，作EF⊥DP于点F，连结AF．求证：DF-EF=$\sqrt{2}$AF；
（3）请你在备用图中画图探究：当P为射线EC上任意一点（P不与点E重合）时，作EF⊥DP于点F，连结AF，线段DF、EF与AF之间有怎样的数量关系？直接写出你的结论．

10．

甲船从A港顺流到P港，乙船从P港逆流到A港，两船同时出发（两船在静水中速度相同），甲、乙两船与P港的距离y（千米）与所用时间x（小时）之间的函数图象如图，请结合图象信息解答下列问题：
（1）求船在静水中的流速和水流的速度；
（2）求点F坐标；
（3）某人乘甲船由A港顺流而下到B港，然后按原路又逆流而上到C港，用去了4小时，已知若A港、C港间的距离为40千米，求A、B两港间的距离．

17．在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b），把余下的部分剪拼成一个矩形，通过计算两个图形阴影部分的面积，验证了一个等式，这个等式是
a²-b²=（a+b）（a-b）．
请你利用这个公式计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{9{9}^{2}}$）（1-$\frac{1}{10{0}^{2}}$）

14．

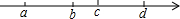如图，a，b，c，d在数轴上的位置如图所示，且b-c=-4．
（1）化简下列各式：
①|a-c|=c-a；②|d-b|=d-b；③|c-b|=c-b．
（2）若bc＜0，化简|a+b|-|b+d|+|c+d|-|a+c|．
（3）P，Q，M，N分别从a，b，c，d表示的点同时出发，P，Q向数轴负方向运动，M，N向数轴正方向运动，P点的运动速度为5个单位/秒，Q点的运动速度为2个单位/秒．M的运动速度为3个单位/秒，N的运动速度为4个单位/秒，若a+2b+d=0，判断在运动的过程中，P，Q，M，N四点表示的数的和是否发生变化？若是，求出其值；若不是，说明理由．

15．抛物线y=-x²+mx+1与直线y=-2的交点个数为2个．

试题分类