题目内容
15．抛物线y=-x2+mx+1与直线y=-2的交点个数为2个．分析 由题意抛物线y=-x2+mx+1与直线y=-2联立方程构成一元二次方程，利用△与0的关系判定即可．
解答 解：假设y=-x2+mx+1与直线y=-2有交点，
则-x2+mx+1=-2，
整理得x2-mx-3=0，
∵△=m2+12＞0，
∴方程必有两个不相等的实数根，
即抛物线y=-x2+mx+1与直线y=-2的交点个数为2个．
故答案为：2．
点评 此题主要考查一元二次方程与函数的关系，已知两函数相交，把他们转化为方程求根的问题，再根据根的判别式判定即可．
练习册系列答案
相关题目
5．
如图所示，在Rt△ABC中，已知∠A=90°，AB=6，BC=8cm，DE垂直平分BC，则BE的长是（ ）
如图所示，在Rt△ABC中，已知∠A=90°，AB=6，BC=8cm，DE垂直平分BC，则BE的长是（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 以上答案都不对 |
如图，在直角△ABC中，∠C=90°，AC=4，BC=3，D是AC的中点，点E是AB边上的一动点，点F是射线BC上一动点，且∠FDE=90°，设AE=x，CF=y．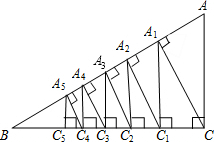
如图，在Rt△BCA中，∠C=90°，AC=3，BC=4，过点C作CA1⊥AB，垂足为点A1，再过点A1作A1C1⊥BC，垂足为点C1，…按以上的方法继续作下去，得到Rt△A5C5C4，求线段A5C5的长．
如图，AB∥CD，FG平分∠EFD，∠1=80°，则∠2=40°．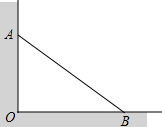
如图所示，在建筑工地上，为了支撑一堵墙，用一根5m的木材，顶端撑在墙上，底端撑在地面上，图中OB=4m．现在为了增加支撑的效果，底端先前移，顶端向上移，若移动距离相等，则应移动多少米？