题目内容
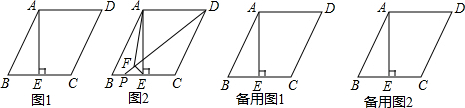
20.如图1,在?ABCD中,AE⊥BC于E,E恰为BC的中点,AE=2BE(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF.求证:DF-EF=$\sqrt{2}$AF;
(3)请你在备用图中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
分析 (1)根据AE=2BE,由题意得出BC=2BE,得出BC=AE,由平行四边形的性质得出即可;
(2)在DP上截取DH=EF,连结AH,由SAS证明△ADH≌△AEF,得出∠HAD=∠FAE,AH=AF,得出∠FAH═90°,由等腰直角三角形的性质得出FH=$\sqrt{2}$AF,即可得出结论;
(3)①当P为线段EC上任意一点(P不与点E重合)时,在PD的延长线上截取DH=EF,连结AH,由SAS证明△ADH≌△AEF,得出∠HAD=∠FAE,AH=AF,得出∠FAH=90°,由等腰直角三角形的性质得出FH=$\sqrt{2}$AF,即可得出结论;
②当P为EC延长线上任意一点(P不与点E重合)时,在PD的延长线上截取DH=EF,连结AH,由SAS证明△ADH≌△AEF,得出∠HAD=∠FAE,AH=AF,得出∠FAH═90°,由等腰直角三角形的性质得出FH=$\sqrt{2}$AF,即可得出结论.
解答 证明:(1)∵E为BC的中点,
∴BC=2AE,
∵AE=2BE,
∴AE=BC,
∵ABCD是平行四边形,
∴AD=BC,
∴AD=AE;
(2)在DP上截取DH=EF,连结AH,如图1所示:
∵四边形ABCD是平行四边形,AE⊥BC,
∴∠EAD=90°,
∵EF⊥PD,∠AGD=∠EGF,
∴∠ADH=∠AEF,
在△ADH和△AEF中,$\left\{\begin{array}{l}{AD=AE}\\{∠ADH=∠AEF}\\{DH=EF}\end{array}\right.$,
∴△ADH≌△AEF(SAS),
∴∠HAD=∠FAE,AH=AF,
∴∠FAH═90°,
在Rt△FAH中,AH=AF
∴$FH=\sqrt{2}AF$,
∴$FH=FD-HD=FD-EF=\sqrt{2}AF$,
即:$DF-EF=\sqrt{2}AF$;
(3)分两种情况:
①当P为线段EC上任意一点(P不与点E重合)时,$DF+EF=\sqrt{2}AF$;理由如下:
在PD的延长线上截取DH=EF,连结AH,如图2所示: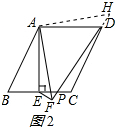 ∵四边形ABCD是平行四边形,AE⊥BC,
∵四边形ABCD是平行四边形,AE⊥BC,
∴∠EAD=90°,
∵EF⊥PD,
∴∠EFD=90°,
∴∠AEF+∠ADF=180°,
∴∠ADH=∠AEF,
在△ADH和△AEF中,$\left\{\begin{array}{l}{AD=AE}\\{∠ADH=∠AEF}\\{DH=EF}\end{array}\right.$,
∴△ADH≌△AEF(SAS),
∴∠HAD=∠FAE,AH=AF,
∴∠FAH=90°,
在Rt△FAH中,AH=AF,HF=$\sqrt{2}$AF,HF=DH+DF=EF+DF,
即:DF+EF=$\sqrt{2}$AF;
②当P为EC延长线上任意一点(P不与点E重合)时,
$EF-FD=\sqrt{2}AF$,理由如下:
在PD的延长线上截取DH=EF,连结AH,如图3所示: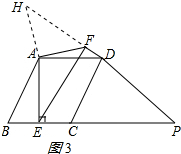 ∵四边形ABCD是平行四边形,AE⊥BC,
∵四边形ABCD是平行四边形,AE⊥BC,
∴∠EAD=90°,∠ADH=∠P,
∵EF⊥PD,
∴∠EFP=90°,
∴∠P+∠PEF=∠PEF+∠AEF=90°,
∴∠ADH=∠AEF,
在△ADH和△AEF中,$\left\{\begin{array}{l}{AD=AE}\\{∠ADH=∠AEF}\\{DH=EF}\end{array}\right.$,
∴△ADH≌△AEF(SAS),
∴∠HAD=∠FAE,AH=AF,
∴∠FAH═90°,
在Rt△FAH中,AH=AF,HF=$\sqrt{2}$AF,HF=DH-DF=EF-DF,
即:EF-DF=$\sqrt{2}$AF.
点评 本题是四边形综合题目,考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度,特别是(3)中,需要进行分类讨论才能得出结果.

| A. | b+1 | B. | b-1 | C. | -b+1 | D. | -b-1 |
 如图所示,在Rt△ABC中,已知∠A=90°,AB=6,BC=8cm,DE垂直平分BC,则BE的长是( )
如图所示,在Rt△ABC中,已知∠A=90°,AB=6,BC=8cm,DE垂直平分BC,则BE的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 以上答案都不对 |
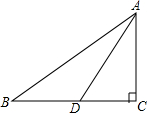 Rt△ABC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是( )
Rt△ABC的角平分线AD交BC于点D,CD=2,则点D到AB的距离是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

 已知二次函数y=x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2-2x+m=0的解为x1=-1,x2=3.
已知二次函数y=x2-2x+m的部分图象如图所示,则关于x的一元二次方程x2-2x+m=0的解为x1=-1,x2=3.