题目内容
14.方程x2-2x-3=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有且只有一个实数根 | D. | 没有实数根 |
分析 根据根的判别式得出△=b2-4ac,套入数据求出△的值,由此即可得出结论.
解答 解:在方程x2-2x-3=0中,
△=b2-4ac=(-2)2-4×1×(-3)=16>0,
故该方程有两个不相等的实数根.
故选A.
点评 本题考查了根的判别式,解题的关键是求出b2-4ac的值.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的正负确定根的个数是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
5.下列运算结果正确的是( )
| A. | $\frac{a}{b}$÷$\frac{c}{d}$=$\frac{ac}{bd}$ | B. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=1 | ||
| C. | ($\frac{2a}{a-b}$)2=$\frac{4{a}^{2}}{{a}^{2}-{b}^{2}}$ | D. | $\frac{{m}^{4}}{{n}^{5}}$•$\frac{{n}^{4}}{{m}^{3}}$=$\frac{m}{n}$ |
2.已知|a+1|+$\sqrt{7+b}$=0,则a+b=( )
| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
19.二次三项式3x2-2x-6的值为3,则x2-$\frac{2}{3}$x+6的值为( )
| A. | 18 | B. | 12 | C. | 9 | D. | 7 |
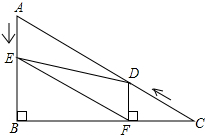 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF. 如图,线段MN将长方形纸分成面积相等的两部分,沿MN将这张长方形纸对折后得到图(2),将图(2)沿对称轴对折,得到图(3),已知图(3)所覆盖的面积占长方形纸面积的$\frac{3}{10}$,阴影部分面积为6平方厘米,长方形的面积是多少?
如图,线段MN将长方形纸分成面积相等的两部分,沿MN将这张长方形纸对折后得到图(2),将图(2)沿对称轴对折,得到图(3),已知图(3)所覆盖的面积占长方形纸面积的$\frac{3}{10}$,阴影部分面积为6平方厘米,长方形的面积是多少?