题目内容
9. 如图,线段MN将长方形纸分成面积相等的两部分,沿MN将这张长方形纸对折后得到图(2),将图(2)沿对称轴对折,得到图(3),已知图(3)所覆盖的面积占长方形纸面积的$\frac{3}{10}$,阴影部分面积为6平方厘米,长方形的面积是多少?
如图,线段MN将长方形纸分成面积相等的两部分,沿MN将这张长方形纸对折后得到图(2),将图(2)沿对称轴对折,得到图(3),已知图(3)所覆盖的面积占长方形纸面积的$\frac{3}{10}$,阴影部分面积为6平方厘米,长方形的面积是多少?
分析 由翻折的性质得出阴影部分重合的次数,空白部分重合的次数,设长方形的面积为x,然后用两种不同的方法表示出空白部分的面积,最后列方程求解即可.
解答 解:由翻折的性质可知:阴影部分重合两次,空白部分重合4次.
设长方形的面积为x,则覆盖的面积为$\frac{3}{10}$x,空白部分的面积为($\frac{3}{10}x-6$).
根据题意得$\frac{3}{10}x$-6=$\frac{x-6×2}{4}$.
解得:x=60.
答;长方形的面积是60.
点评 本题主要考查的是翻折变换,用含x的式子表示出空白部分的面积,并列出方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.方程x2-2x-3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有且只有一个实数根 | D. | 没有实数根 |
17.在平面直角坐标系中,将点(-2,3)关于原点的对称点向右平移2个单位长度得到的点的坐标是( )
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
18. 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
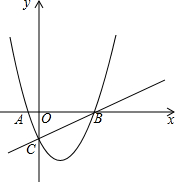 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数.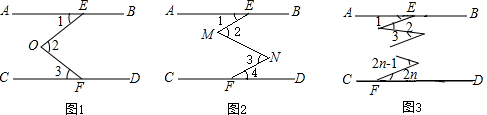
 如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.
如图,将△ABC绕点B顺时针旋转40°得到△DBE,若此时点A的对应点D恰好落在边AC上,且∠ABE=90°,则∠C的度数为60°.
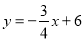 与
与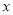 轴、
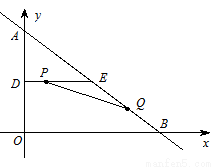
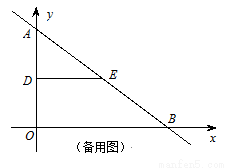
轴、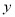 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为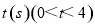 .
.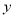 (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;