题目内容
4.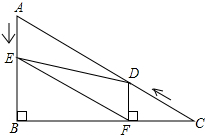 如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
分析 (1)由∠DFC=90°,∠C=30°,证出DF=t=AE;
(2)先证明四边形AEFD为平行四边形.得出AB=5,AD=AC-DC=10-2t,若△DEF为等边三角形,则?AEFD为菱形,得出AE=AD,t=10-2t,求出t=$\frac{10}{3}$;
(3)分三种情况讨论:①∠EDF=90°时;②∠DEF=90°时;③∠EFD=90°时,此种情况不存在;分别求出t的值即可.
解答 解:(1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF;
(2)能;
理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
∵∠C=30°,AC=10,
∴AB=5,BC=5$\sqrt{3}$
∴AD=AC-DC=10-2t,
若使△DEF能够成为等边三角形,
则平行四边形AEFD为菱形,则AE=AD,
∴t=10-2t,
∴t=$\frac{10}{3}$;
即当t=$\frac{10}{3}$时,△DEF为等边三角形;
(3)当t=$\frac{2}{5}$或4时,△DEF为直角三角形;
理由如下:
①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE.即10-2t=2t,
∴t=$\frac{5}{2}$;
②∠DEF=90°时,由(2)知EF∥AD,
∴∠ADE=∠DEF=90°.
∵∠A=90°-∠C=60°,
∴AD=AE•cos60°.
即10-2t=$\frac{1}{2}$t,
∴t=4;
③∠EFD=90°时,
∵DF⊥BC,
∴点运动到点B处,用了AB÷1=5秒中,
同时点D也运动5秒钟,点D就和点A重合,
点F也就和点B重合,
点D,E,F不能构成三角形.
此种情况不存在;
综上所述,当t=$\frac{5}{2}$或4时,△DEF为直角三角形.
点评 本题是四边形综合题,主要考查了平行四边形、菱形、矩形的判定与性质以及锐角三角函数的知识;考查学生综合运用定理进行推理和计算的能力;特别注意(3)中分类讨论三种情况,分别求出t的值,避免漏解

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案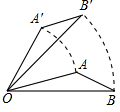 如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
| A. | 2楼4号 | B. | 大学路19号 | C. | 北偏东60° | D. | 东经111°北纬40° |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有且只有一个实数根 | D. | 没有实数根 |
 ②
② ③
③ ④
④ 中,一元二次方程的个数是( )
中,一元二次方程的个数是( )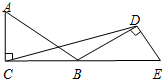 如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°.
如图,△ABC绕着顶点B顺时针旋转150°得△EBD,连结CD,若∠ACB=90°,∠ABC=30°,则∠BDC的度数是15°. 已知:抛物线y=x2+2mx+m,m为常数.
已知:抛物线y=x2+2mx+m,m为常数.