题目内容
14.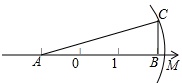 如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )| A. | 2.1 | B. | $\sqrt{10}$-1 | C. | $\sqrt{10}$ | D. | $\sqrt{10}$+1 |
分析 先根据勾股定理求出AB的长,进而可而出结论.
解答 解:∵△ABC中,∠B=90°,AB=3,BC=1,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
∵A点表示-1,
∴M点表示$\sqrt{10}$-1.
故选B.
点评 本题考查的是勾股定理及实数与数轴,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知⊙O的半径为6cm,点O到直线l的距离为5cm,则直线l与⊙O( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相切或相交 |
2. 如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么$\widehat{AB}$与$\widehat{CD}$的数量关系是( )
如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么$\widehat{AB}$与$\widehat{CD}$的数量关系是( )
 如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么$\widehat{AB}$与$\widehat{CD}$的数量关系是( )
如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么$\widehat{AB}$与$\widehat{CD}$的数量关系是( )| A. | $\widehat{AB}$=$\widehat{CD}$ | B. | $\widehat{AB}$>$\widehat{CD}$ | C. | $\widehat{AB}$<$\widehat{CD}$ | D. | 无法确定 |
9.某小区9月底的房价为3.2万元/m2,同年11月底的房价为3万元/m2.设平均每月降价的百分率为 x,可列方程.( )
| A. | 3.2(1+x)2=3 | B. | 3.2(1-x)2=3 | C. | 3(1+x)2=3.2 | D. | 3(1-x)2=3.2 |
19. 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,AB=7.8cm,那么线段MN的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,AB=7.8cm,那么线段MN的长等于( )
 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,AB=7.8cm,那么线段MN的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,AB=7.8cm,那么线段MN的长等于( )| A. | 5.4 cm | B. | 5.6 cm | C. | 5.8 cm | D. | 6 cm |
6.若关于x的不等式$\left\{\begin{array}{l}{x-m≤0}\\{5-2x<1}\end{array}\right.$共有2个整数解,则m的取值范围( )
| A. | 4<m<5 | B. | 4<m≤5 | C. | 4≤m≤5 | D. | 4≤m<5 |
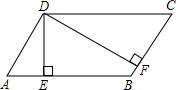 如图,在平行四边形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四边形ABCD的边长AB=9,BC=6,求平行四边形ABCD的面积.
如图,在平行四边形ABCD中,DE⊥AB,DF⊥BC,若DE+DF=10,平行四边形ABCD的边长AB=9,BC=6,求平行四边形ABCD的面积.