题目内容
2．
如图，A，B，C，D是⊙O上的四个点，AD∥BC．那么$\widehat{AB}$与$\widehat{CD}$的数量关系是（ ）| A． | $\widehat{AB}$=$\widehat{CD}$ | B． | $\widehat{AB}$＞$\widehat{CD}$ | C． | $\widehat{AB}$＜$\widehat{CD}$ | D． | 无法确定 |
分析 根据平行线的性质得∠DAC=∠ACB，根据圆周角定理得$\widehat{AB}$=$\widehat{CD}$．
解答 
证明：连接AC，
∵AD∥BC，
∴∠DAC=∠ACB，
∴$\widehat{AB}$=$\widehat{CD}$．
故选：A．
点评 本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
13．计算（-$\frac{1}{3}$）-2的值，正确的是（ ）
| A． | $\frac{1}{9}$ | B． | -$\frac{1}{9}$ | C． | 9 | D． | -9 |
10．
乒乓球是一种世界流行的球类体育项目，某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间，并将统计结果绘制成如图所示的条形统计图，则这50名学生该周平均参加乒乓球运动的时间为（ ）
乒乓球是一种世界流行的球类体育项目，某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间，并将统计结果绘制成如图所示的条形统计图，则这50名学生该周平均参加乒乓球运动的时间为（ ）| A． | 1.5小时 | B． | 1.8小时 | C． | 2小时 | D． | 2.5小时 |
17．下列结论正确的是（ ）
| A． | xyz的系数为0 | B． | 3x2-x+1 中一次项系数为-1 | ||
| C． | a2b3c的次数为5 | D． | a2-33是一个三次二项式 |
7．sin 30°等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
14．
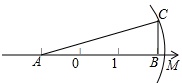如图，△ABC中，∠B=90°，AB=3，BC=1，AB在数轴上，以点A为圆心，AC长为半径作弧，交数轴的正半轴于点M，则M表示的数为（ ）
如图，△ABC中，∠B=90°，AB=3，BC=1，AB在数轴上，以点A为圆心，AC长为半径作弧，交数轴的正半轴于点M，则M表示的数为（ ）| A． | 2.1 | B． | $\sqrt{10}$-1 | C． | $\sqrt{10}$ | D． | $\sqrt{10}$+1 |
11．方程x2=4的解是（ ）
| A． | x=2 | B． | x=-2 | C． | x1=1，x2=4 | D． | x1=2，x2=-2 |
12．已知有理数a和它的相反数之间有2009个整数，则（ ）
| A． | 1004＜a＜1005 | B． | 1004≤a＜1005 | ||
| C． | 1004＜a＜1005或-1005≤a＜-1004 | D． | 1004≤a＜1005或-1005＜a≤-1004 |