题目内容
5.等腰三角形的周长为24cm,其中有两边的差为2cm,求这个等腰三角形的三边之长.分析 已知等腰三角形的周长为24cm,两边之差为2cm,但没有明确指明底边与腰谁大,因此要分两种情况,分类讨论.
解答 解:设三角形的腰为xcm,底为ycm,
根据题意得$\left\{\begin{array}{l}{2x+y=24}\\{x-y=2}\end{array}\right.$或$\left\{\begin{array}{l}{2x+y=24}\\{y-x=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{26}{3}}\\{y=\frac{20}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{22}{3}}\\{y=\frac{28}{3}}\end{array}\right.$,
故等腰三角形的腰与底边的长分别为:$\frac{26}{3}$cm,$\frac{26}{3}$cm,$\frac{20}{3}$cm或$\frac{22}{3}$cm,$\frac{22}{3}$cm,$\frac{28}{3}$cm.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.正六边形的周长为6,则它的面积为( )
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
13.计算(-$\frac{1}{3}$)-2的值,正确的是( )
| A. | $\frac{1}{9}$ | B. | -$\frac{1}{9}$ | C. | 9 | D. | -9 |
20.下列各式中,不能用平方差公式分解因式的是( )
| A. | y2-49x2 | B. | $\frac{1}{49}-{x^4}$ | C. | -m2-n2 | D. | $\frac{1}{4}{(p+q)^2}-9$ |
10. 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
 乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )
乒乓球是一种世界流行的球类体育项目,某校刘老师随机调查了50名学生在一周中参加乒乓球运动的时间,并将统计结果绘制成如图所示的条形统计图,则这50名学生该周平均参加乒乓球运动的时间为( )| A. | 1.5小时 | B. | 1.8小时 | C. | 2小时 | D. | 2.5小时 |
17.下列结论正确的是( )
| A. | xyz的系数为0 | B. | 3x2-x+1 中一次项系数为-1 | ||
| C. | a2b3c的次数为5 | D. | a2-33是一个三次二项式 |
14.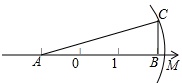 如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
 如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )
如图,△ABC中,∠B=90°,AB=3,BC=1,AB在数轴上,以点A为圆心,AC长为半径作弧,交数轴的正半轴于点M,则M表示的数为( )| A. | 2.1 | B. | $\sqrt{10}$-1 | C. | $\sqrt{10}$ | D. | $\sqrt{10}$+1 |
15.算式22+22+22+22可化为( )
| A. | 24 | B. | 82 | C. | 28 | D. | 216 |
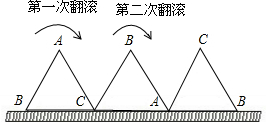 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.