题目内容
18.若关于x的一元二次方程-x2+2ax+2-a=0的一根x1≥1,另一根x2≤-1,则抛物线y=-x2+2ax+2-a的顶点到x轴距离的最小值是$\frac{16}{9}$.分析 先根据关于x的一元二次方程-x2+2ax+2-a=0的一根x1≥1,另一根x2≤-1求出a的取值范围,再得出抛物线y=-x2+2ax+2-a顶点的纵坐标表达式,把a的取值代入即可.
解答 解:∵关于x的一元二次方程-x2+2ax+2-a=0的一根x1≥1,另一根x2≤-1,
∴$\left\{\begin{array}{l}f(1)≥0\\ f(-1)≥0\end{array}\right.$,即$\left\{\begin{array}{l}-1+2a+2-a≥0\\-1-2a+2-a≥0\end{array}\right.$,解得-1≤a≤$\frac{1}{3}$.
∵抛物线y=-x2+2ax+2-a的顶点纵坐标=$\frac{-4(2-a)-4{a}^{2}}{-4}$=2-a+a2,
当a=-1时,2-a+a2=2+1+4=7;
当a=$\frac{1}{3}$时,2-$\frac{1}{3}$+$\frac{1}{9}$=$\frac{16}{9}$,
∵7>$\frac{16}{9}$,
∴顶点到x轴距离的最小值是$\frac{16}{9}$.
故答案为:$\frac{16}{9}$.
点评 本题考查的是抛物线与x轴的交点,熟知一元二次方程的根与抛物线与x轴的交点之间的关系是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.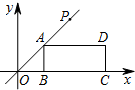 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )| A. | 0<b<3 | B. | -3<b<0 | C. | -6<b<-3 | D. | -3<b<3 |
3. 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
 如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )
如图,点O是△ABC的内心,∠A=62°,则∠BOC=( )| A. | 59° | B. | 31° | C. | 124° | D. | 121° |
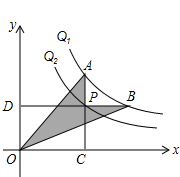 如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.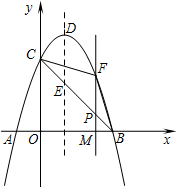 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D. 如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.
如图,抛物线y=x2-4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q,与x轴交于点T.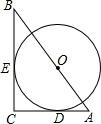 如图,⊙O的圆心在Rt△ABC的斜边AB上,且⊙O分别与边AC、BC相切于D、E两点,已知AC=3,BC=4,则⊙O的半径r=$\frac{12}{7}$.
如图,⊙O的圆心在Rt△ABC的斜边AB上,且⊙O分别与边AC、BC相切于D、E两点,已知AC=3,BC=4,则⊙O的半径r=$\frac{12}{7}$.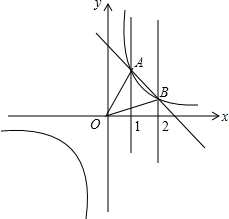 已知一次函数y1=-x+3与反比例函数y2=$\frac{2}{x}$的图象交于点A(1,2),B(2,1).
已知一次函数y1=-x+3与反比例函数y2=$\frac{2}{x}$的图象交于点A(1,2),B(2,1).