题目内容
8.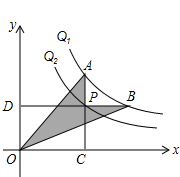 如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
如图,反比例函数y=$\frac{5}{x}$和y=$\frac{3}{x}$,在第一象限内图象依次是Q1和Q2.设点P在Q2,直线PC⊥x轴于点C,交Q1于点A,直线PD⊥y轴于点D,交Q1于点B,连结OA,OB,则图中阴影部分的面积为2.
分析 连接OP.设点P坐标为(m,$\frac{3}{m}$),则点A(m,$\frac{5}{m}$),点B($\frac{5m}{3}$,$\frac{3}{m}$),根据S阴=S△PAO+S△POB即可解决问题.
解答  解:连接OP.设点P坐标为(m,$\frac{3}{m}$),则点A(m,$\frac{5}{m}$),点B($\frac{5m}{3}$,$\frac{3}{m}$),
解:连接OP.设点P坐标为(m,$\frac{3}{m}$),则点A(m,$\frac{5}{m}$),点B($\frac{5m}{3}$,$\frac{3}{m}$),
∴S阴=S△PAO+S△POB
=$\frac{1}{2}$•PA•OC+$\frac{1}{2}$•PB•OD
=$\frac{1}{2}$•($\frac{5}{m}$-$\frac{3}{m}$)•m+$\frac{1}{2}$•($\frac{5m}{3}$-m)•$\frac{3}{m}$=2.
故答案为2.
点评 本题考查反比例函数的比例系数k的几何意义,解题的关键是利用参数表示相应的点的坐标,学会利用分割法求四边形面积,属于中考常考题型.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a+a2=a3 | B. | a6b÷a2=a3b | C. | (a-b)2=a2-b2 | D. | (-ab3)2=a2b6 |
13. 如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
 如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )
如图,正方形OABC的边长为6,A,C分别位于x轴、y轴上,点P在AB上,CP交OB于点Q,函数y=$\frac{k}{x}$的图象经过点Q,若S△BPQ=$\frac{1}{4}$S△OQC,则k的值为( )| A. | -12 | B. | 12 | C. | 16 | D. | 18 |
20. 如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
 如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )
如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2的度数为( )| A. | 35° | B. | 15° | C. | 10° | D. | 5° |
 如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论: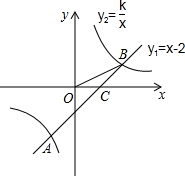 如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.
如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.