题目内容
6.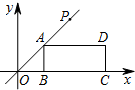 如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )
如图,在平面直角坐标系中,矩形ABCD的边BC在x轴的正半轴上,点B在点C的左侧,直线y=kx经过点A(3,3)和点P,且OP=6$\sqrt{2}$.将直线y=kx沿y轴向下平移得到直线y=kx+b,若点P落在矩形ABCD的内部,则b的取值范围是( )| A. | 0<b<3 | B. | -3<b<0 | C. | -6<b<-3 | D. | -3<b<3 |
分析 作PE⊥AD于E交BC于F,先求出直线y=kx以及点P坐标,再确定点E、F坐标,代入y=x+b中即可解决问题.
解答 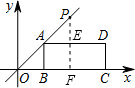 解:如图作PE⊥AD于E交BC于F,
解:如图作PE⊥AD于E交BC于F,
∵直线y=kx经过点A(3,3),
∴k=1,
∴直线为y=x,设点P坐标(a,a),
∵OP=6$\sqrt{2}$,
∴a2+a2=72,
∴a2=36,
∵a>0,
∴a=6.
∴点P坐标(6,6),点E(6,3),点F(6,0),
把点E(6,3),点F(6,0)分别代入y=x+b中,得到b=-3或-6,
∴点P落在矩形ABCD的内部,
∴-6<b<-3.
故选C.
点评 本题考查一次函数有关知识,掌握两条直线平行k值相同,寻找特殊点是解决问题的关键,理解点P在平移过程中与y轴的距离保持不变,属于中考常考题型.

练习册系列答案
相关题目
1.a的倒数是-1.5,则a是( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
11.下列计算正确的是( )
| A. | x3•x5=x15 | B. | x4÷x=x3 | C. | 3x2•4x2=12x2 | D. | (x5)2=x7 |
 如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论:
如图(1)所示,E为矩形ABCD的边AD上一点动点P、Q同时从点B出发,点P以1cm/秒的速度沿折线BE-ED-DC运动到点C时停止,点Q以2cm/秒的速度沿BC运动到点C时停止.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(其中曲线OG为抛物线的一部分,其余各部分均为线段),则下列结论: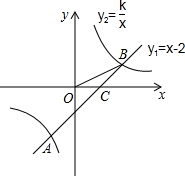 如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.
如图,一次函数y1=x-2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$,点B的坐标为(m,n),求反比例函数的解析式.
 直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.
直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=40°,则∠2=85°.