题目内容
17.解不等式$\left\{\begin{array}{l}{3x+2≥-1①}\\{4x+1≤5②}\end{array}\right.$请结合题意填空,完全本题的解答
(1)解不等式①,得x≥-1.
(2)解不等式②,得x≤1.
(3)把不等式①和②的解集在数轴上表示出来.
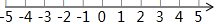
(4)原不等式组的解集为-1≤x≤1.
分析 先根据不等式基本性质求出两个不等式的解集,再将不等式解集表示在数轴上,根据解集在数轴上的表示求其公共解.
解答 解:(1)解不等式①,得:x≥-1,
(2)解不等式②,得:x≤1,
(3)把不等式①和②的解集表示在数轴上,如图:
(4)∴原不等式组的解集为:-1≤x≤1;
故答案为:(1)x≥-1;(2)x≤1;(4)-1≤x≤1.
点评 本题考查的是一元一次不等式组的整数解,会求一元一次不等式组的解集是解决此类问题的关键.求不等式组的解集,借助数轴找公共部分或遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.长春市总面积为20565平方公里,20565这个数用科学记数法表示为( )
| A. | 20.565×102 | B. | 2.0565×103 | C. | 2.0565×104 | D. | 0.20565×104 |
12.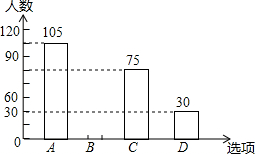 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
结合上述统计图表,回答下列问题:
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
(1)本次抽查的学生共300人,x=30%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请估计该校喜爱“篮球”这项球类运动的学生约有多少人?
(3)学校决定举行一次乒乓球比赛,甲,乙,丙,丁四人参加比赛,从四人中随机抽取两人打第一场比赛,请用树状图或列表法所抽到的两人恰好是甲和丁的概率.
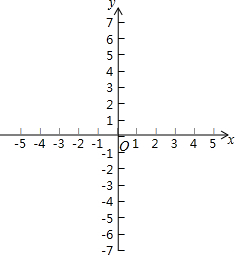 在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0).
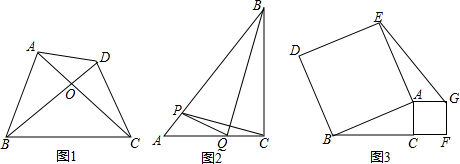
在平面直角坐标系中,二次函数y=x2+mx+2m-7的图象经过点(1,0). 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.