题目内容
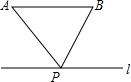点P是直线L上的一点，线段AB∥L，能使PA+PB取得最小值的点P的位置应满足的条件是（ ）| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
考点：轴对称-最短路线问题
专题：
分析：作点A关于直线l的对称点A′，根据轴对称确定最短路线问题，连接A′B与直线l的交点即为使PA+PB取得最小值的点P，根据轴对称的性质可得PA=PA′，根据等边对等角可得∠A′=∠PAA′，再根据等角的余角相等求出∠PAB=∠PBA，然后根据等角对等边解答．
解答：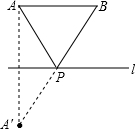
解：如图，作点A关于直线l的对称点A′，
连接A′B与直线l的交点即为使PA+PB取得最小值的点P，
由轴对称的性质得，PA=PA′，
所以，∠A′=∠PAA′，
∵线段AB∥L，AA′⊥直线L，
∴AA′⊥AB，
∴∠PA′A+∠PAB=90°，∠A′+∠B=90°，
∴∠PAB=∠PBA，
∴PA=PB．
故选C．
解：如图，作点A关于直线l的对称点A′，连接A′B与直线l的交点即为使PA+PB取得最小值的点P，
由轴对称的性质得，PA=PA′，
所以，∠A′=∠PAA′，
∵线段AB∥L，AA′⊥直线L，
∴AA′⊥AB，
∴∠PA′A+∠PAB=90°，∠A′+∠B=90°，
∴∠PAB=∠PBA，
∴PA=PB．
故选C．
点评：本题考查了轴对称确定最短路线问题，平行线的性质，等角的余角相等的性质，熟练掌握最短路线的确定方法是解题的关键．
练习册系列答案
相关题目
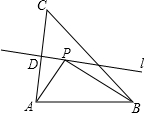如图，AC的垂直平分线l交AC于点D，BC=4，点P在直线l上，则PB+PA的最小值是
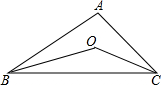如图，O是△ABC的内心，∠BOC=100°，则∠A=
已知：△ABC