题目内容
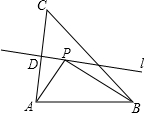如图，AC的垂直平分线l交AC于点D，BC=4，点P在直线l上，则PB+PA的最小值是考点：轴对称-最短路线问题,线段垂直平分线的性质
专题：
分析：连接PC，根据线段垂直平分线上的点到两端点的距离相等可得PA=PC，然后求出PA+PB=PC+PB，再根据轴对称确定最短路线问题，点P为BC与直线l的交点时PB+PA有最小值．
解答：
解：如图，连接PC，
∵直线l为AC的垂直平分线，
∴PA=PC，
∴PA+PB=PC+PB，
∴点P为BC与直线l的交点时PB+PA有最小值，
∵BC=4，
∴PB+PA的最小值是4．
故答案为：4．
解：如图，连接PC，∵直线l为AC的垂直平分线，
∴PA=PC，
∴PA+PB=PC+PB，
∴点P为BC与直线l的交点时PB+PA有最小值，
∵BC=4，
∴PB+PA的最小值是4．
故答案为：4．
点评：本题考查了轴对称确定最短路线问题，线段垂直平分线上的点到两端点的距离相等的性质，熟记性质以及最短路线的确定方法是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知：∠1和∠2，作一个角，使它等于∠1-∠2．
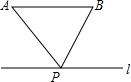点P是直线L上的一点，线段AB∥L，能使PA+PB取得最小值的点P的位置应满足的条件是（ ）| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
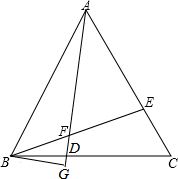已知△ABC是等边三角形，BD=CE，BG⊥AD于G，求证：