题目内容
已知函数y=(n+2)xn2+n-4是关于x的二次函数.
(1)求满足条件的n的值;
(2)当n为何值时,抛物线有最低点?求出这个最低点的坐标,并写出y随x的增大而增大的x的取值范围.
(1)求满足条件的n的值;
(2)当n为何值时,抛物线有最低点?求出这个最低点的坐标,并写出y随x的增大而增大的x的取值范围.
考点:二次函数的性质,二次函数的定义
专题:计算题
分析:(1)根据二次函数的定义得n+2≠0且n2+n-4=2,然后解一元二次方程即可得到n的值;
(2)根据二次函数的性质求解.
(2)根据二次函数的性质求解.
解答:解:(1)根据题意得n+2≠0且n2+n-4=2,解n2+n-4=2得n1=-3,n2=2,
所以n的值为-3或2;
(2)当n+2>0,即n>-2时,抛物线开口向上,抛物线有最低点,所以n=2,
此时解析式为y=4x2,这个最低点的坐标为(0,0),当x>0时,y随x的增大而增大.
所以n的值为-3或2;
(2)当n+2>0,即n>-2时,抛物线开口向上,抛物线有最低点,所以n=2,
此时解析式为y=4x2,这个最低点的坐标为(0,0),当x>0时,y随x的增大而增大.
点评:本题考查了二次函数y=ax2+bx+c(a≠0)的性质:熟练掌握二次函数的性质是解决此类问题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知正比例函数y=kx(k<0)的图象上两点A(x1,y1)、B(x2,y2),且x1<x2,下列说法正确的是( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、不能确定 |
36.33°可化成( )
| A、36°30′3″ |
| B、36°3′ |
| C、36°30′30″ |
| D、36°19′48″ |
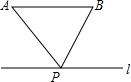 点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )
点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
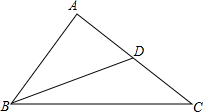 如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.
如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.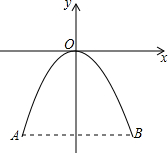 如图,一座抛物线形的拱桥,其形状可以用y=-x2来描述.
如图,一座抛物线形的拱桥,其形状可以用y=-x2来描述.