题目内容
a是不为1的有理数,我们把
称为a的差倒数.如:2的差倒数是
=-1,-1的差倒数是
=
. 已知a1=-
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2014= .
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 3 |
考点:规律型:数字的变化类
专题:新定义,规律型
分析:根据差倒数的定义分别求出a2、a3、a4、…,不难发现,每3个数为一个循环组依次循环,用2014除以3,根据商和余数的情况确定a2014即可.
解答:解:∵a1=-
,
∴a2=
=
,
a3=
=4,
a4=
=-
,
…,
∴每3个数为一个循环组依次循环,
∵2014÷3=671余1,
∴a2014是第672循环组的第1个数,与a1相同,
∴a2014=-
.
故答案为:-
.
| 1 |
| 3 |
∴a2=
| 1 | ||
1-(-
|
| 3 |
| 4 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-4 |
| 1 |
| 3 |
…,
∴每3个数为一个循环组依次循环,
∵2014÷3=671余1,
∴a2014是第672循环组的第1个数,与a1相同,
∴a2014=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
点评:本题是对数字变化规律的考查,读懂题目信息,理解“差倒数”的定义并求出每3个数为一个循环组依次循环是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
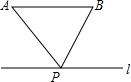 点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )
点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
绝对值最小的实数是( )
| A、正数中最小的数 |
| B、有理数中最小的数 |
| C、整数中最小的数 |
| D、自然数中最小的数 |
 如图,直角△AOB顺时针旋转后与△COD重合,若∠AOD=126°,则旋转角度是
如图,直角△AOB顺时针旋转后与△COD重合,若∠AOD=126°,则旋转角度是
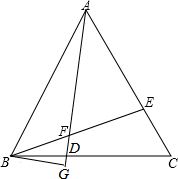 已知△ABC是等边三角形,BD=CE,BG⊥AD于G,求证:
已知△ABC是等边三角形,BD=CE,BG⊥AD于G,求证: