题目内容
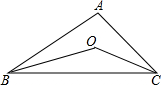 如图,O是△ABC的内心,∠BOC=100°,则∠A=
如图,O是△ABC的内心,∠BOC=100°,则∠A=考点:三角形的内切圆与内心
专题:计算题
分析:先根据三角形的内心的定义得到∠OBC=
∠ABC,∠OCB=
∠ACB,再根据三角形的内角和定理求出∠OBC+∠OCB=180°-∠BOC=80°,则有∠ABC+∠ACB=160°,然后再利用三角形内角和计算∠A的度数.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵O是△ABC的内心,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∵∠OBC+∠OCB=180°-∠BOC=180°-100°=80°,
∴
(∠ABC+∠ACB)=80°,
即∠ABC+∠ACB=160°,
∴∠A=180°-(∠ABC+∠ACB)=180°-160°=20°;
故答案为20°.
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OBC+∠OCB=180°-∠BOC=180°-100°=80°,
∴
| 1 |
| 2 |
即∠ABC+∠ACB=160°,
∴∠A=180°-(∠ABC+∠ACB)=180°-160°=20°;
故答案为20°.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
36.33°可化成( )
| A、36°30′3″ |
| B、36°3′ |
| C、36°30′30″ |
| D、36°19′48″ |
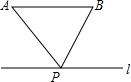 点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )
点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
 如图,已知直线l及其两侧两点A、B,在直线l上求作一点P,使PA=PB;提醒:用直尺和圆规按要求作图,不写作法,但保留作图痕迹.
如图,已知直线l及其两侧两点A、B,在直线l上求作一点P,使PA=PB;提醒:用直尺和圆规按要求作图,不写作法,但保留作图痕迹.