题目内容
已知30°<α<β<90°,化简
-|cosβ-
|+|1-cosα|.
| (cosα-cosβ)2 |
| ||
| 2 |
考点:二次根式的性质与化简,锐角三角函数的增减性
专题:计算题
分析:根据α与β的范围,利用余弦函数的性质判断出绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果.
解答:解:∵30°<α<β<90°,
∴cosα>cosβ,cosβ<
,1-cosα>0,
则原式=cosα-cosβ+cosβ-
+1-cosα=1-
.
∴cosα>cosβ,cosβ<
| ||
| 2 |
则原式=cosα-cosβ+cosβ-
| ||
| 2 |
| ||
| 2 |
点评:此题考查了二次根式的性质与化简,以及锐角三角函数的增减性,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
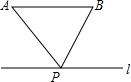 点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )
点P是直线L上的一点,线段AB∥L,能使PA+PB取得最小值的点P的位置应满足的条件是( )| A、点P为点A到直线L的垂线的垂足 |
| B、点P为点B到直线L的垂线的垂足 |
| C、PB=PA |
| D、PB=AB |
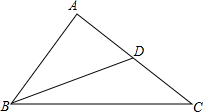 如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.
如图,AB=4,BC=6,BD为△ABC的中线,求BD的范围.