题目内容
20.如图1,在△ABC中,AB=AC=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为$\sqrt{2}$;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,则当△MPQ的面积等于四边形MPAQ的面积的一半时,四边形MPAQ的形状为正方形,此时BP=1.
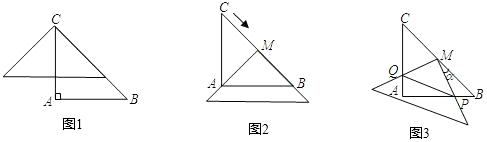
分析 (1)M是BC的中点,三角板沿C→B方向平移的距离为CM,根据勾股定理可求BC,那么CM可求;
(2)方法一、连AM,分别证明△MAQ≌△MBP和△MAP≌△MCQ,那么四边形MPAQ的面积S就是△ABC面积的一半;
方法二、先判断出S正方形ADME=$\frac{1}{2}$S△ABC,再求出三角形ABC的面积,最后判断出△DMQ≌△EMP即可得出结论;
(3)用四边形MPAQ的面积减去△APQ可得△MPQ的面积,设AQ=PB=x,AP=2-x,据此列出△MPQ的面积为$\frac{1}{2}$列出方程即可求出BP,进而可以判断四边形MPAQ的形状.
解答 (1)解:(1)BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∴CM=$\frac{1}{2}$BC=$\sqrt{2}$故三角板沿C→B方向平移的距离为:$\sqrt{2}$;
故答案为:$\sqrt{2}$;
(2)答:四边形MPAQ的面积S不变.
解法1:连接AM,
∵AB=AC=2,∠A=90°,
∴S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×2×2=2
又由(1)知,点M是BC中点
∴∠CAM=∠BAM=∠B=45°,AM⊥BC,
∴AM=BM,∠BMP+∠PMA=90°
∴S△ABM=$\frac{1}{2}$S△ABC=1
又∠AMQ+∠PMA=90°
∴∠AMQ=∠BMP
∴△AMQ≌△BMP
∴S四边形MPAQ=S△ABM=1,
解法2:如图3, 作MD⊥AC于D,作ME⊥AB于E,
作MD⊥AC于D,作ME⊥AB于E,
∵AB=AC=2,∠A=90°
∴∠B=∠C=45°,四边形ADME是矩形,
S△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×2×2=2
又∵点M是BC中点
∴Rt△CMD≌Rt△BME
∴四边形ADME是正方形,易求S正方形ADME=$\frac{1}{2}$S△ABC=1
∴MD=ME,∠DMQ+∠QME=90°,
又∠EMP+∠QME=90°
∴∠DMQ=∠EMP
∴△DMQ≌△EMP
∴S四边形MPAQ=S正方形ADME=1,
(3)设AQ=PB=x,AP=2-x,
S△MPQ=S四边形MAPQ-S△APQ=1-$\frac{1}{2}$AQ•AP=1-$\frac{1}{2}$x(2-x)=$\frac{1}{2}$x2-x+1=$\frac{1}{2}$
解得,x=1.
∴PB=1,
∴AQ=PB=AP=1,
∴点P是AB的中点,
∵M是BC中点,
∴PM∥AQ,
∴∠MPA=90°,
∵∠PAQ=∠PMQ=90°,
∴四边形MPAQ是矩形,
∵AQ=AP,
∴矩形MPAQ是正方形,
故答案为:正方形,1.
点评 此题是几何变换综合题,主要考查了旋转的性质、全等三角形的判定、等腰直角三角形的性质、正方形的判定三角形的面积公式,解(2)的关键是找出几个图形的面积关系,解(3)的关键是判断出四边形MPAQ是矩形.


| A. | 9cm2 | B. | 18cm2 | C. | 27cm2 | D. | 72cm2 |

问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1(图3) | 8 | 1 | 8 |
| 多边形2(图4) | 7 | 3 | 11 |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
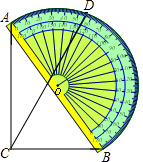 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )| A. | 63° | B. | 54° | C. | 36° | D. | 27° |
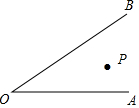 如图,点P在∠AOB内.
如图,点P在∠AOB内.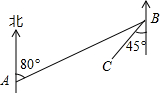 一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.
一艘轮船从点A出发沿北偏东80°,方向航行到点B后再沿西南方向航行,则∠ABC=35°.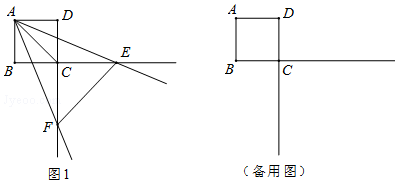
 如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.请你判断AD和BE的位置关系,并说明理由.
如图,AB∥CD,AE平分∠BAD,CD与AE相交于F,∠CFE=∠E.请你判断AD和BE的位置关系,并说明理由.