题目内容
15．
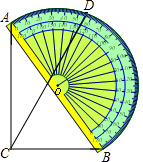如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD的度数为（ ）| A． | 63° | B． | 54° | C． | 36° | D． | 27° |
分析 先根据圆周角定理得到∠ACD=$\frac{1}{2}$∠AOD=27°，然后利用互余求解．
解答 解：∵一块直角三角板ABC的斜边AB与量角器的直径重合，
∴点A、B、C、D都在以AB为直径的圆上，
∵点D对应54°，即∠AOD=54°，
∴∠ACD=$\frac{1}{2}$∠AOD=27°，
∴∠BCD=90°-∠ACD=63°．
故选A．
点评 本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了圆周角定理．
练习册系列答案
相关题目
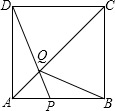如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连结DP交AC于点Q．
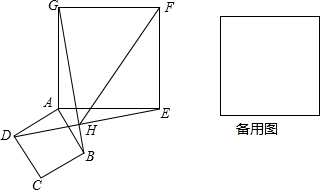如图，已知正方形ABCD、AEFG边长分别为$\sqrt{2}$cm、2cm，将正方形ABCD绕点A旋转，连接BG、DE相交于点H．
如图，已知△ABC是圆内接三角形，若∠OCB=15°，则∠A=75度．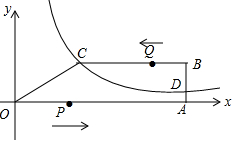
如图，在直角坐标系中，O是原点，点C的坐标为C（12，5），点A在x轴的正半轴上，四边形OABC是直角梯形，经过点C的反比例函数的图象交AB于点D，且点D的纵坐标为2．