题目内容
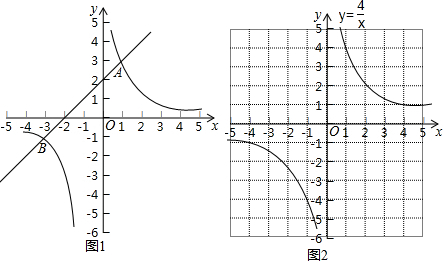
17.阅读下面材料:如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$交于A(1,3)和B(-3,-1)两点.
观察图象可知:
①当x=-3或1时,y1=y2;
②当-3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>$\frac{k}{x}$的解集.
有这样一个问题:求不等式x3+4x2-x-4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2-x-4>0的解集进行了探究.
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x-1>$\frac{4}{x}$;
当x<0时,原不等式可以转化为x2+4x-1<$\frac{4}{x}$;
(2)构造函数,画出图象
设y3=x2+4x-1,y4=$\frac{4}{x}$,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=$\frac{4}{x}$如图2所示,请在此坐标系中画出抛物线y3=x2+4x-1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为±1和-4;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2-x-4>0的解集为x>1或-4<x<-1.
分析 (2)首先确定二次函数的对称轴,然后确定两个点即可作出二次函数的图象;
(3)根据图象即可直接求解;
(4)根据已知不等式x3+4x2-x-4>0即当x>0时,x2+4x-1>$\frac{4}{x}$,;当x<0时,x2+4x-1<$\frac{4}{x}$,根据图象即可直接写出答案.
解答 解:(2)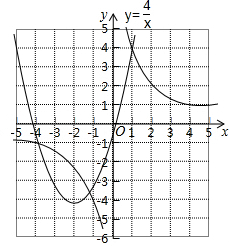 ;
;
(3)两个函数图象公共点的横坐标是±1和-4.
则满足y3=y4的所有x的值为±1和-4.
故答案是:±1和-4;
(4)不等式x3+4x2-x-4>0即当x>0时,x2+4x-1>$\frac{4}{x}$,此时x的范围是:x>1;
当x<0时,x2+4x-1<$\frac{4}{x}$,则-4<x<-1.
故答案是:x>1或-4<x<-1.
点评 本题考查了二次函数与不等式,正确理解不等式x3+4x2-x-4>0即当x>0时,x2+4x-1>$\frac{4}{x}$,;当x<0时,x2+4x-1<$\frac{4}{x}$,分成两种情况讨论是本题的关键.

练习册系列答案
相关题目
9.有一个数值转换器,原理如下:

当输入的x=64时,输出的y等于( )

当输入的x=64时,输出的y等于( )
| A. | 2 | B. | 8 | C. | $2\sqrt{2}$ | D. | $3\sqrt{2}$ |
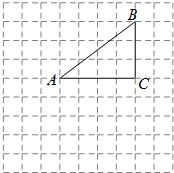 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.