题目内容
20. 如图,已知点A,B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,且P为AC的中点,若△ABP的面积为2,则k=-8.
如图,已知点A,B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,且P为AC的中点,若△ABP的面积为2,则k=-8.
分析 由△ABP的面积为2,知BP•AP=4.根据反比例函数y=$\frac{k}{x}$中k的几何意义,知本题|k|=OC•AC,由反比例函数的性质,结合已知条件P是AC的中点,得出OC=BP,AC=2AP,进而求出k的值.
解答 解:∵△ABP的面积为$\frac{1}{2}$•BP•AP=2,
∴BP•AP=4,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A,B在反比例函数y=$\frac{k}{x}$(x<0)的图象上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴|k|=OC•AC=BP•2AP=8.
故答案为:-8.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
14.下列图形都是按照一定规律组成,第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形,…,依此规律,第六个图形中三角形的个数是( )


| A. | 20 | B. | 26 | C. | 32 | D. | 38 |
5.将二次函数y=2x2的图象向左平移2个单位,得到的新图象对应的函数表达式为( )
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |
9. 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
 如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x,当y1<y2时,x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>2 | C. | x<0或x>4 | D. | 0<x<4 |
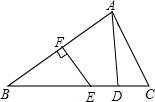 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC. 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)