题目内容
18. 如图,AB=AE,∠1=∠2,∠C=∠D,判断线段BC与线段DE是否相等,并说明理由.
如图,AB=AE,∠1=∠2,∠C=∠D,判断线段BC与线段DE是否相等,并说明理由.
分析 先利用∠1=∠2得到∠BAC=∠DAE,然后根据“AAS”证明△ACB≌△ADE,则根据全等三角形的性质得DE=BC.
解答 解:BC=DE,
理由:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠CAE,
即∠BAC=∠EAD,
在△ABC与△AED中,$\left\{\begin{array}{l}{∠BAC=∠EAD}\\{∠C=∠D}\\{AB=AE}\end{array}\right.$,
∴△ABC≌△AED,
∴BC=DE.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
6. 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.将二次函数y=2x2的图象向左平移2个单位,得到的新图象对应的函数表达式为( )
| A. | y=2x2+2 | B. | y=2(x+2)2 | C. | y=2x2-2 | D. | y=2(x-2)2 |

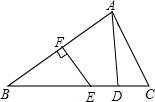 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC. 如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点
如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点