题目内容
5. 如图,在Rt△ABC中,∠ACB=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C′的位置,其中A′,B′分别是A,B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,求∠BDC的度数.
如图,在Rt△ABC中,∠ACB=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C′的位置,其中A′,B′分别是A,B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,求∠BDC的度数.
分析 利用三角形内角和定理得出∠ABC=55°,再利用旋转的性质结合等腰三角形的性质得出∠CB′B=∠B′BC,进而求出答案.
解答 解:∵∠ACB=90°,∠A=35°,
∴∠ABC=55°,
∵以直角顶点C为旋转中心,将△ABC旋转到△A′B′C′的位置,
∴∠B′=∠CBA=55°,BC=B′C,
∴∠CB′B=∠B′BC=55°,
∴∠A′BD=180°-55°-55°=70°,
∴∠BDC=∠A′+∠A′BD=35°+70°=105°.
点评 此题主要考查了旋转的性质以及三角形内角和定理,正确得出∠CB′B=∠B′BC=55°是解题关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
6.a,b是有理数,如果|a+b|=a-b,那么对下列结论:
(1)a一定不是负数 (2)b可能是负数
判断正确的是( )
(1)a一定不是负数 (2)b可能是负数
判断正确的是( )
| A. | 只有(1)正确 | B. | 只有(2)正确 | C. | (1)(2)都不正确 | D. | (1)(2)都正确 |
 、
、 与直线
与直线 相交,给出下列条件:
相交,给出下列条件:
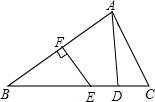 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC.
如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,∠CAD=20°,∠ACB的补角是110°.求证:BE=AC. 如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化?
如图,在△ABC中,∠ABC=45°,H是高AD和高BE的交点,则BH和AC的大小关系如何?并说明理由.猜想:若∠ABC=135°,其他条件不变,则BH和AC的大小关系将发生什么变化? 如图所示:
如图所示:
 如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)
如图,某建筑物BC上有一旗杆AB,小明在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面的距离EF为1.6m,求旗杆AB的高度.(结果精确到0.1m,参考数据$\sqrt{2}$≈1.41,sin52°≈0.79,tan52°≈1.28)