题目内容
11.在△ABC中,已知AB=a2,BC=4a,AC=b2-4,且a,b都是大于3的奇数,则a与b的大小关系是( )| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
分析 由三角的三边关系即可得出a-2<b<a+2,再结合a,b都是大于3的奇数即可得出a=b.
解答 解:∵在△ABC中,已知AB=a2,BC=4a,AC=b2-4,
∴$\left\{\begin{array}{l}{{a}^{2}+4a>{b}^{2}-4}\\{{a}^{2}+{b}^{2}-4>4a}\\{4a+{b}^{2}-4>{a}^{2}}\end{array}\right.$,
∴a-2<b<a+2.
∵a,b都是大于3的奇数,
∴a=b.
故选C.
点评 本题考查了三角形三边关系以及因式分解的应用,根据三角形的三边关系找出a-2<b<a+2是解题的关键.

练习册系列答案
相关题目
13.将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )
| A. | y=5(x-2)2+3 | B. | y=5(x+2)2+3 | C. | y=5(x-2)2-3 | D. | y=5(x+2)2-3 |
 如图,点A、B在直线l的两旁,在直线l上求作一点P,使|PA-PB|的值最大.(不写画法,请保留作图痕迹)
如图,点A、B在直线l的两旁,在直线l上求作一点P,使|PA-PB|的值最大.(不写画法,请保留作图痕迹)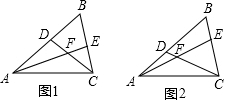
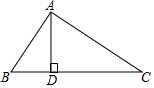 如图,∠BAC=∠ADB=90°,则下列结论
如图,∠BAC=∠ADB=90°,则下列结论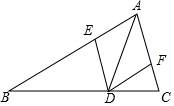 如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.
如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.