题目内容
1.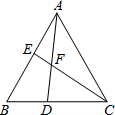 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.(1)当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数,若变化,写出其变化规律;
(2)当点D、E运动到BC、AB的延长线上时,(1)中的结论是否改变?说明理由.
分析 (1)根据已知条件得到△ABD≌△CAE,由全等三角形的性质得到∠AEC=∠ADB,推出△AEF∽△ADB,根据相似三角形的性质即可得到结论;
(2)根据外角的性质得到∠CBE=∠ACD=120°,推出△BCE≌△ACD,由全等三角形的性质得到∠E=∠D,证得△BCE∽△CDF,由相似三角形的性质得到∠CFD=∠CBE=120°,根据外角的性质即可得到结论.
解答 解:(1)不变,
在△ABD与△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠BAC}\\{BD=AE}\end{array}\right.$,
∴△ABD≌△CAE,
∴∠AEC=∠ADB,
∵∠BAD=∠EAF,
∴△AEF∽△ADB,
∴∠AFE=∠ABC=60°;
(2)不变,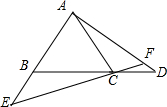
∵∠ABC=∠ACB=60°,
∴∠CBE=∠ACD=120°,
∵BD=AE,AB=BC,
∴BE=CD,
在△BCE与△ACD中,
$\left\{\begin{array}{l}{BE=CD}\\{∠CBE=∠ACD}\\{BC=AC}\end{array}\right.$,
∴△BCE≌△ACD,
∴∠E=∠D,
∵∠BCE=∠DCF,
∴△BCE∽△CDF,
∴∠CFD=∠CBE=120°,
∴∠AFE=60°.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,相似三角形的判定和性质,正确的识别图形是解题的关键.

练习册系列答案
相关题目
6.如图,若将如图正方形剪成四块,恰好能拼成如图的矩形,则$\frac{a}{b}$等于( )
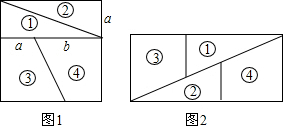

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
11.若x2-5x+6=(x+a)(x+b),a,b的值可能为( )
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
10.有一锐角相等的两个直角三角形一定( )
| A. | 全等 | B. | 相似 | ||
| C. | 既不全等也不相似 | D. | 相似但不全等 |
11.下列各度数不是多边形的内角和的是( )
| A. | 1700° | B. | 540° | C. | 1800° | D. | 10800° |