题目内容
4.某苹果生产基地,用30名工人进行采摘或加工苹果,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4000元;加工成
罐头出售每吨获利10000元.采摘的工人每人可以采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设
有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式.
(2)如何分配工人才能获利最大?最大利润为多少?
分析 (1)采摘苹果的工人有x名,加工苹果的工人有30-x,根据采摘的苹果重量大于等于加工成罐头的苹果的重量得出关于x的一元一次不等式组,解不等式组即可得出x的取值范围,再根据总利润=出售罐头的利润+出售水果的利润可得出y关于x的解析式;
(2)根据函数的单调性,结合x的取值范围即可解决最值问题.
解答 解:(1)采摘苹果的工人有x名,加工苹果的工人有30-x,
每天能采摘苹果的重量为0.4x吨,每天能加工苹果的重量为0.3(30-x)=-0.3x+9吨.
根据题意有$\left\{\begin{array}{l}{0.4x≥-0.3x+9}\\{30-x≥0}\end{array}\right.$,
解得:12$\frac{6}{7}$≤x≤30,
∵x为整数,
∴13≤x≤30.
总利润y=10000(-0.3x+9)+4000[0.4x-(-0.3x+9)]=-200x+54000(13≤x≤30,且x为整数).
(2)∵y=-200x+54000在x取值范围内单调递减,
∴当x=13时,y去最大值,最大值为51400,
此时30-x=17.
故分配13名员工采摘苹果,17名员工加工罐头才能获得最大利润,最大利润是51400元.
点评 本题考查了一元一次不等式组的应用以及一次函数的应用,解题的关键是:(1)解不等式组得出x的取值范围;(2)根据函数的单调性解决最值问题.本题属于中档题,(1)有点难度,需要通过数量之间的关系找出一元一次不等式组,解不不等式组得出x的取值范围,此处学生经常忘记函数的解析式往往要带上值域;(2)在(1)的基础上利用函数的单调性解决最值问题,难度不大,单若(1)不对,此问也得不到分值,故该题的重点是通过解不等式组得出x的取值范围.

练习册系列答案
相关题目
19.[a,b]为一次函数y=ax+b(a≠0)的“云数”.若“云数”为[1,m-2]的一次函数是正比例函数,则关于x的方程$\frac{1}{x-1}$+$\frac{1}{m}$=m的解为x=3.
9.某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件,第二个月如果单价不变,预计仍可以售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降1元,可多售出10件,但最低单价应高于购进的价格;第二月结束后.批发商核对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表(不需化简)
(2)如果批发商希望通过销售这批T恤获利8000元,那么第二个月的单价应该是多少?
(3)如果批发商希望通过销售这批T恤获利最大,那么第二个月的单价应是多少元?最大利润为多少?
(1)填表(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量 | 200 | 200+10x | 800-200-(200+10x) |
(3)如果批发商希望通过销售这批T恤获利最大,那么第二个月的单价应是多少元?最大利润为多少?

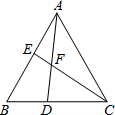 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.