题目内容
11.若x2-5x+6=(x+a)(x+b),a,b的值可能为( )| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
分析 利用十字相乘法对等式的左边进行因式分解.
解答 解:∵x2-5x+6=(x-2)(x-3),x2-5x+6=(x+a)(x+b),
∴(x-2)(x-3)=(x+a)(x+b),
∴a=-2,b=-3;或a=-3,b=-2.
故选:B.
点评 本题考查了十字相乘法分解因式,运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程,本题需要进行多次因式分解,分解因式一定要彻底.

练习册系列答案
相关题目
19.[a,b]为一次函数y=ax+b(a≠0)的“云数”.若“云数”为[1,m-2]的一次函数是正比例函数,则关于x的方程$\frac{1}{x-1}$+$\frac{1}{m}$=m的解为x=3.
5.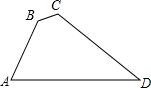 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )| A. | $6\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $4\sqrt{2}$ | D. | $4\sqrt{3}$ |
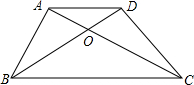 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
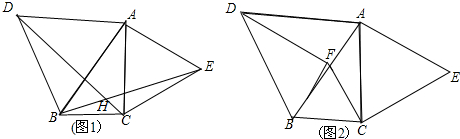
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积. 如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.
如图,已知DB∥FG∥EC,∠ABD=60°,∠ACE=60°,AP是∠BAC的平分线,求∠PAG的度数.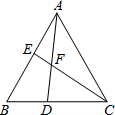 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.