题目内容
13.已知有理数m,n满足(m+n)2=9,(m-n)2=1.求下列各式的值.(1)mn;
(2)m2+n2.
分析 (1)已知等式利用完全平方公式化简,相减即可求出mn的值;
(2)已知等式利用完全平方公式化简,相加即可求出m2+n2的值.
解答 解:(m+n)2=m2+n2+2mn=9①,(m-n)2=m2+n2-2mn=1②,
(1)①-②得:4mn=8,
则mn=2;
(2)①+②得:2(m2+n2)=10,
则m2+n2=5.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18.已知一个菱形的周长是20cm,两条对角线的比是4:3,则这个菱形的面积是( )
| A. | 12cm2 | B. | 96cm2 | C. | 48cm2 | D. | 24cm2 |
19.[a,b]为一次函数y=ax+b(a≠0)的“云数”.若“云数”为[1,m-2]的一次函数是正比例函数,则关于x的方程$\frac{1}{x-1}$+$\frac{1}{m}$=m的解为x=3.
5.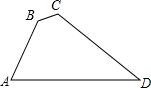 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )| A. | $6\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $4\sqrt{2}$ | D. | $4\sqrt{3}$ |
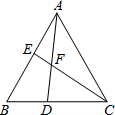 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与BC交于点F.
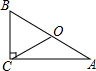 如图,Rt△ABC中,∠ACB=90°,CO是中线,延长CO到D,使DO=CO,连接AD、BD.
如图,Rt△ABC中,∠ACB=90°,CO是中线,延长CO到D,使DO=CO,连接AD、BD.