题目内容
19.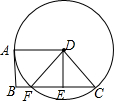 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
分析 欲证明四边形ABED为矩形,只要证明∠DAB=∠ABE=∠DEB=90°即可.
解答  证明:∵AB是⊙D的切线,A是切点,
证明:∵AB是⊙D的切线,A是切点,
∴DA⊥AB,∠DAB=90°,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠ABC=90°,
∵DF=DC,EF=EC,
∴DE⊥BC,
∴∠DEB=90°,
∵∠DAB=∠ABE=∠DEB=90°,
∴四边形ABED是矩形.
点评 本题考查切线的性质、矩形的判定、等腰三角形的性质等知识,掌握矩形的判定方法是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
10.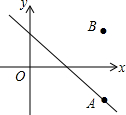 如图,在平面直角坐标系中,直线y=-x+1上一点A关于x轴的对称点为B(2,m),则m的值为( )
如图,在平面直角坐标系中,直线y=-x+1上一点A关于x轴的对称点为B(2,m),则m的值为( )
 如图,在平面直角坐标系中,直线y=-x+1上一点A关于x轴的对称点为B(2,m),则m的值为( )
如图,在平面直角坐标系中,直线y=-x+1上一点A关于x轴的对称点为B(2,m),则m的值为( )| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
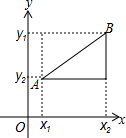 阅读材料
阅读材料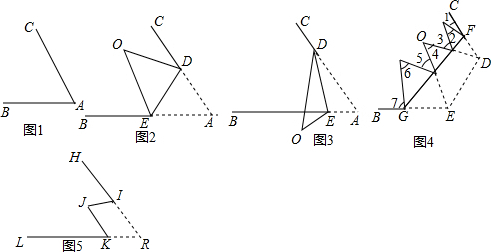
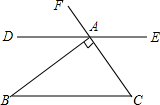 如图,BA⊥FC于A点,过A点作DE∥BC,若∠EAF=125°,则∠B=35°.
如图,BA⊥FC于A点,过A点作DE∥BC,若∠EAF=125°,则∠B=35°.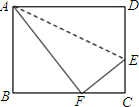 如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.
如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.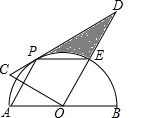 如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.
如图,在Rt△COD中,∠COD=90°,∠D=30°,斜边CD与以AB为直径,O为圆心的半圆相切于点P,OD与半圆交于点E,连接PA,PE,PA与OC交于点F.