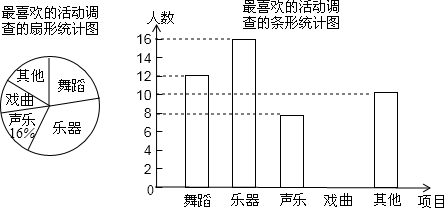
题目内容
7. 阅读材料
阅读材料通过前面的学习我们已经知道了两点之间的距离,点到直线的距离和两条平行线间的距离,那么我们如何在平面直角坐标系中求这些距离呢?
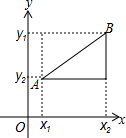
如图1,在平面直角坐标系xOy中,A、B两点的坐标分为A(x1,y1),B(x2,y2),由勾股定理得AB2=|x1-x2|2+|y1-y2|2,所以A、B两点间的距离为AB=$\sqrt{|{x}_{1}-{x}_{2}{|}^{2}+|{y}_{1}-{y}_{2}{|}^{2}}$.这样就可以求出平面直角坐标系中任意两点间的距离.
我们用下面的公式可以求出平面直角坐标系中任意一点到某条直线的距离:
已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$
计算:例如:求点P(-2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x-y+1=0,其中k=1,b=1.
所以点P(-2,1)到直线y=x+1的距离了为d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$=$\frac{|1×(-2)-1+1|}{\sqrt{1+{1}^{2}}}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
根据以上材料,解决下列问题:
(1)已知A(-2,1),B(4,3),求线段AB的长度;
(2)点P(1,1)到直线y=3x-2的距离,并说明点P与直线的位置关系;
(3)点P(2,-1)到直线y=2x-1的距离;
(4)已知直线y=-x+1与y=-x+3平行,求这两条直线的距离.
分析 (1)由A与B的坐标,利用题中的方法求出AB的长即可;
(2)利用点到直线的距离公式求出P在直线的距离,即可作出判断;
(3)利用点到直线的距离公式求出P在直线的距离即可;
(4)从直线y=-x+1上找一个点(1,0),求出该点到y=-x+3的距离,即为两条平行线的距离.
解答 解:(1)∵A(-2,1),B(4,3),
∴AB=$\sqrt{(-2-4)^{2}+(1-3)^{2}}$=2$\sqrt{10}$;
(2)∵直线y=3x-2变形得:3x-y-2=0,
∴点P(1,1)到直线y=3x-2的距离d=$\frac{|3-1-2|}{\sqrt{1+{3}^{2}}}$=0,
则点P在直线上;
(3)∵直线y=2x-1,即2x-y-1=0,k=2,b=1,
∴P(2,-1)到直线y=2x-1的距离d=$\frac{|4+1-1|}{\sqrt{1+{2}^{2}}}$=$\frac{4\sqrt{5}}{5}$;
(4)找出直线y=-x+1上一点(1,0),
∵y=-x+3,即x+y-3=0,k=-1,b=3,
∴(1,0)到直线y=-x+3的距离d=$\frac{|1-0-3|}{\sqrt{1+(-1)^{2}}}$=$\sqrt{2}$,
则两平行线间的距离为$\sqrt{2}$.
点评 此题属于一次函数综合题,弄清题中求两点间的距离以及点到直线的距离方法是解本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.不等式2x+1<3的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |

 如图,直线CD与∠B的一边相交于点E,且CD∥AB,若∠BED=70°,则∠B的度数等于70°.
如图,直线CD与∠B的一边相交于点E,且CD∥AB,若∠BED=70°,则∠B的度数等于70°.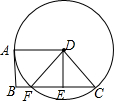 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.