题目内容
11.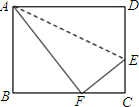 如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.
如图,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已AB=32cm,BC=40cm,求CE的长.
分析 首先求出BF的长度,进而求出FC的长度;根据勾股定理列出关于线段EF的方程,即可解决问题.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=40cm,DC=AB=32cm;∠B=90°,
由题意得:
AF=AD=40cm;DE=EF(设为x),EC=40-x;
由勾股定理得:
BF2=402-322=576,
∴BF=24,CF=40-24=16;
由勾股定理得:
x2=162+(40-x)2,
解得:x=23.2,
∴EC=32-23.2=8.8.
点评 该题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质找出图形中隐含的等量关系;根据有关定理灵活分析、正确判断、准确求解.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
1.如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n=( )
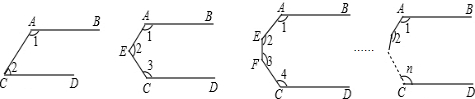

| A. | n•180° | B. | 2n•180° | C. | (n-1)•180° | D. | (n-1)2•180° |

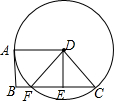 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.