题目内容
14.如图,在一张透明的纸上画了一个∠BAC,且∠BAC=α.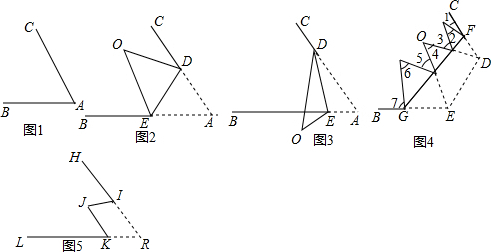
(1)如图2,把纸片∠BAC沿DE折起(DE为折痕),使顶点A在∠BAC的内部,点A的对称点为点O,求证:∠CDO+∠OEB=2α.
(2)如图3,把纸片∠BAC沿DE折起(DE为折痕),使顶点A在∠BAC的外部,点A的对称点为点O写出∠CDO、∠OEB与α的等式关系(只写出答案,无需证明).
(3)如图4,在图2的基础上再以FG为折痕叠纸片,使顶点D、E在∠BAC的内部,且点D、E的对称点分别为点P、Q,求∠CFP+∠PMO+∠ONQ+∠QGB的大小.
(4)如图5,是一个侧“M”形HIJKL.已知:∠HIJ+∠JKL=2∠IJK.分别延长HI、LK交于点R,问∠HRL与∠IJK是否相等?如果相等,则请证明;如果不相等,则说明理由(举一反例).
分析 (1)由平角和对折的性质简单计算∠CDO=180°-2∠ADE即可;
(2)由平角和对折的性质简单计算∠OEB=∠AED-180°即可;
(3)由对折和平角的意义进行简单的计算,
(3)利用几何图形,对折,平角的意义简单的计算.
解答 解:(1)∵如图2,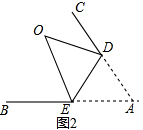
∵把三角形纸片ABC的∠A沿DE折起,点A的对称点为点O,
∴∠CDO+∠OEB
=(180°-2∠ADE)+(180°-2∠AED)
=2(180°-∠ADE-∠AED)=2α;
(2)∠CDO-∠OEB=2α,
理由如下:如图3,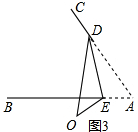
∠CD0-∠OEB
=(180°-2∠ADE)-(2∠AED-180°)
=2(180°-∠ADE-∠AED)
=2α;
(3)∠CFP+PMO+∠ONQ+∠QGB=4α,
理由如下:如图4,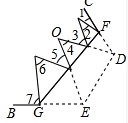
∠CFP+∠PMO+∠ONQ+∠QGB
=(∠CFP+∠PMO)+(∠ONQ+QGB)
=2∠FDM+2∠NEG
=2(∠FDM+NEG)
=4∠BAC
=4α;
(4)∠HRL=∠IJK,
理由如下:如图5,连接JR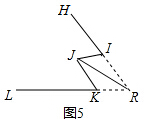
∵∠HIJ+∠JKL
=(∠IRJ+∠IJR)+(∠KRJ+∠KJR)
=(∠IJR+∠KJR)+(∠IRJ+∠KRJ)
=∠IJK+∠IRK
=2∠IJK,
∴∠HRL=∠IJK.
点评 本题是几何变换题,主要考查了对折的性质,本题的关键是从复杂图形分离出有用的部分,本题易出错的地方是,写错角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )| A. | 50° | B. | 40° | C. | 80° | D. | 60° |
4.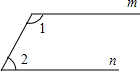 如图,若m∥n,∠1=105°,则∠2=( )
如图,若m∥n,∠1=105°,则∠2=( )
 如图,若m∥n,∠1=105°,则∠2=( )
如图,若m∥n,∠1=105°,则∠2=( )| A. | 75° | B. | 85° | C. | 95° | D. | 105° |
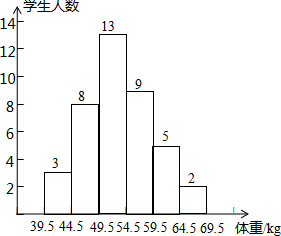 根据某班40名同学的体重频数分布直方图,回答下列问题:
根据某班40名同学的体重频数分布直方图,回答下列问题:
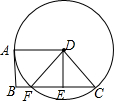 已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.
已知,如图,在梯形ABCD中,AD∥BC,DA=DC.以点D为圆心.DA长为半径的⊙D与AB相切于点A,与BC交于点F,E为CF的中点,求证:四边形ABED为矩形.